Lcm Of 7 4 And 2
Juapaving
Apr 02, 2025 · 5 min read
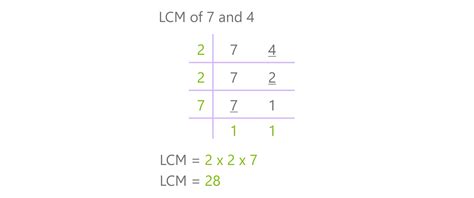
Table of Contents
Understanding the Least Common Multiple (LCM) of 7, 4, and 2
The least common multiple (LCM) is a fundamental concept in mathematics, particularly in number theory and arithmetic. It represents the smallest positive integer that is a multiple of all the given integers. Finding the LCM is crucial in various applications, from simplifying fractions to solving problems involving cycles and periodic events. This article delves into the detailed calculation and application of finding the LCM of 7, 4, and 2, exploring different methods and providing a comprehensive understanding of this important mathematical concept.
What is the Least Common Multiple (LCM)?
Before we dive into calculating the LCM of 7, 4, and 2, let's solidify our understanding of the concept itself. The LCM of a set of integers is the smallest positive integer that is divisible by each of the integers in the set without leaving a remainder. In simpler terms, it's the smallest number that all the given numbers can divide into evenly. For instance, the LCM of 2 and 3 is 6 because 6 is the smallest number that is divisible by both 2 and 3.
Methods for Finding the LCM
Several methods exist for calculating the LCM of a set of integers. We will explore the three most common approaches:
-
Listing Multiples: This method is suitable for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
-
Prime Factorization: This method is efficient for larger numbers. We find the prime factorization of each number and then construct the LCM by taking the highest power of each prime factor present in the factorizations.
-
Greatest Common Divisor (GCD) Method: This method leverages the relationship between the LCM and the greatest common divisor (GCD). The LCM and GCD of two numbers are related by the formula: LCM(a, b) * GCD(a, b) = a * b. This method can be extended to more than two numbers.
Calculating the LCM of 7, 4, and 2 using Different Methods
Now, let's apply these methods to find the LCM of 7, 4, and 2.
Method 1: Listing Multiples
Let's list the multiples of 7, 4, and 2:
- Multiples of 7: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84, ...
- Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60, ...
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, ...
By inspecting the lists, we can see that the smallest common multiple among these three is 28. Therefore, the LCM(7, 4, 2) = 28. This method is straightforward for small numbers, but it becomes less practical as the numbers increase in size.
Method 2: Prime Factorization
This method involves finding the prime factorization of each number and then constructing the LCM.
- Prime factorization of 7: 7 (7 is a prime number)
- Prime factorization of 4: 2²
- Prime factorization of 2: 2
To find the LCM, we take the highest power of each prime factor present in the factorizations:
- The highest power of 2 is 2² = 4
- The highest power of 7 is 7¹ = 7
Therefore, the LCM(7, 4, 2) = 2² * 7 = 4 * 7 = 28. This method is more efficient than listing multiples, especially for larger numbers.
Method 3: Greatest Common Divisor (GCD) Method
This method is particularly useful when dealing with larger numbers. First, we need to find the GCD of the numbers. We can use the Euclidean algorithm for this purpose.
Let's find the GCD of 7, 4, and 2. Since 7 is a prime number and it doesn't divide 4 or 2, the GCD(7, 4, 2) = 1.
Now, we can use the relationship between LCM and GCD:
LCM(a, b, c) = (a * b * c) / GCD(a, b, c) (This formula is an extension of the two-number case and requires a bit of caution when applying it to more than two numbers. It only directly works if the GCD of the numbers is not 1. When it is 1, we'll have to rely on the other methods.)
In our case, this formula isn't directly applicable because GCD(7, 4, 2) = 1. Hence, it's more efficient to use either the listing multiples or prime factorization method.
Applications of LCM
The concept of LCM has numerous applications across various fields:
-
Fraction Addition and Subtraction: Finding the LCM of the denominators is essential when adding or subtracting fractions. It allows us to find a common denominator, simplifying the calculation process.
-
Cyclic Events: LCM is useful in determining when cyclical events will coincide. For example, if two events occur every 7 days and 4 days respectively, the LCM will indicate when they will occur on the same day.
-
Scheduling and Time Management: LCM helps in scheduling tasks or events that repeat at different intervals. This is useful for project management, planning events, or any situation where cyclical tasks need coordination.
-
Music and Rhythm: In music, LCM helps determine the least common multiple of different note values and rhythmic patterns. This ensures rhythmic consistency and harmony.
-
Gear Ratios: In mechanical engineering, LCM is used in calculating gear ratios and synchronizing the rotation speed of different gears.
-
Computer Science: LCM finds applications in algorithms and data structures, particularly in problems involving synchronization and periodic operations.
Conclusion
Finding the LCM of 7, 4, and 2 is a straightforward exercise that demonstrates the fundamental principles behind this mathematical concept. The different methods presented—listing multiples, prime factorization, and the GCD method—provide various approaches to tackling LCM problems. The choice of method depends on the complexity of the numbers involved and the context of the problem. Understanding LCM is crucial not only for solving mathematical problems but also for tackling real-world applications across various disciplines. Its importance extends to fractions, scheduling, rhythm, and even mechanical engineering, making it a valuable tool in numerous fields. Mastering the concept of LCM enhances mathematical skills and problem-solving capabilities in a wide range of applications.
Latest Posts
Latest Posts
-
Compare And Contrast Pulmonary Circulation With Systemic Circulation
Apr 03, 2025
-
Does Photosynthesis Take Place Primarily In Plant Leaves
Apr 03, 2025
-
A Sphere Is Inscribed In A Cube
Apr 03, 2025
-
Balanced Equation Of Hcl And Naoh
Apr 03, 2025
-
What Is 0 35 As A Fraction
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 7 4 And 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
