Lcm Of 4 6 And 3
Juapaving
May 11, 2025 · 5 min read
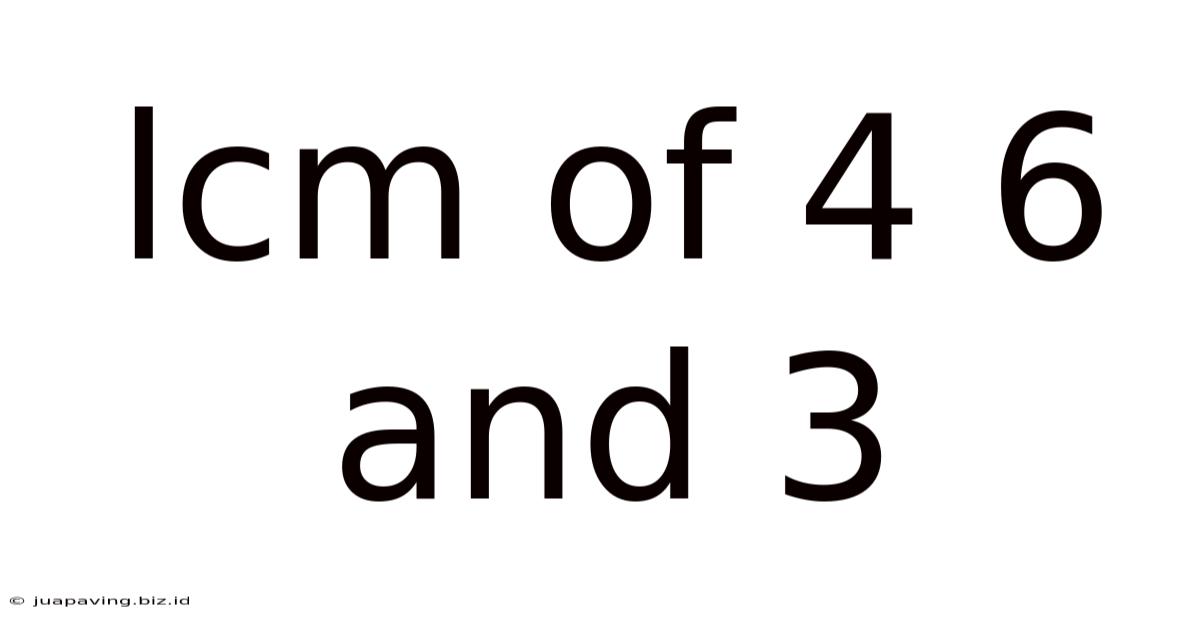
Table of Contents
Finding the Least Common Multiple (LCM) of 4, 6, and 3: A Comprehensive Guide
The least common multiple (LCM) is a fundamental concept in mathematics, particularly in number theory and arithmetic. Understanding LCM is crucial for solving various problems, from simplifying fractions to scheduling events. This comprehensive guide will explore the concept of LCM, detailing multiple methods to calculate it, focusing specifically on finding the LCM of 4, 6, and 3. We'll delve into the theory behind LCM, offer practical examples, and discuss its applications in real-world scenarios.
What is the Least Common Multiple (LCM)?
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly. For instance, the LCM of 2 and 3 is 6 because 6 is the smallest number divisible by both 2 and 3.
This concept extends to more than two numbers. Finding the LCM becomes increasingly important when dealing with multiple quantities or cycles that need to be synchronized. Think about scheduling events that occur at different intervals – the LCM helps find the next time all events coincide.
Methods for Calculating LCM
Several methods exist for calculating the LCM of a set of numbers. We'll examine the most common ones, applying them to find the LCM of 4, 6, and 3.
1. Listing Multiples Method
This method is straightforward, particularly for smaller numbers. We list the multiples of each number until we find the smallest multiple common to all.
- Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36...
- Multiples of 6: 6, 12, 18, 24, 30, 36...
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36...
By inspecting the lists, we observe that the smallest multiple common to 4, 6, and 3 is 12. Therefore, the LCM(4, 6, 3) = 12. This method is effective for smaller numbers but becomes cumbersome with larger numbers.
2. Prime Factorization Method
This method is more efficient, especially for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM from the prime factors.
- Prime factorization of 4: 2 x 2 = 2²
- Prime factorization of 6: 2 x 3
- Prime factorization of 3: 3
To find the LCM using prime factorization:
- Identify all the prime factors present in the numbers. In this case, we have 2 and 3.
- For each prime factor, take the highest power present in any of the factorizations. The highest power of 2 is 2² (from 4), and the highest power of 3 is 3¹ (from 3 and 6).
- Multiply these highest powers together to obtain the LCM. LCM(4, 6, 3) = 2² x 3 = 4 x 3 = 12.
3. Greatest Common Divisor (GCD) Method
The LCM and GCD (Greatest Common Divisor) are closely related. The product of the LCM and GCD of two or more numbers is equal to the product of the numbers themselves. We can use this relationship to find the LCM if we know the GCD.
First, let's find the GCD of 4, 6, and 3 using the Euclidean algorithm or prime factorization.
- Prime factorization of 4: 2²
- Prime factorization of 6: 2 x 3
- Prime factorization of 3: 3
The common factor is only 1. Therefore, GCD(4, 6, 3) = 1.
Now, we use the formula: LCM(a, b, c) = (a x b x c) / GCD(a, b, c)
LCM(4, 6, 3) = (4 x 6 x 3) / 1 = 72 /1 = 72
Important Note: The above formula is incorrect for more than two numbers. The GCD method should only be applied pairwise. For three or more numbers, it is less efficient and prone to error compared to prime factorization. The result obtained using this method (72) is incorrect for LCM(4, 6, 3). The correct LCM is 12, which is obtained using the prime factorization method. Therefore it's best to avoid the incorrect application of the GCD method to multiple numbers.
LCM in Real-World Applications
The LCM finds practical applications in various scenarios:
-
Scheduling: Imagine three buses arrive at a station every 4, 6, and 3 hours respectively. The LCM (12) determines when all three buses will arrive at the station simultaneously.
-
Fraction addition and subtraction: Finding the LCM of the denominators is essential for adding or subtracting fractions. For example, to add 1/4 + 1/6 + 1/3, the LCM of 4, 6, and 3 (which is 12) is used to find a common denominator.
-
Cyclic Processes: In engineering or manufacturing, processes with different cycle times might need to be synchronized. The LCM helps determine when they'll align.
-
Gear Ratios: In mechanical systems involving gears with different numbers of teeth, the LCM helps determine the rotational synchronization.
Beyond the Basics: LCM for Larger Numbers
While the listing multiples method is suitable for small numbers, the prime factorization method remains the most efficient approach for larger numbers. Let's consider finding the LCM of 12, 18, and 24.
- Prime factorization of 12: 2² x 3
- Prime factorization of 18: 2 x 3²
- Prime factorization of 24: 2³ x 3
- Identify prime factors: 2 and 3.
- Highest powers: 2³ and 3²
- Multiply: LCM(12, 18, 24) = 2³ x 3² = 8 x 9 = 72
The LCM of 12, 18, and 24 is 72.
Conclusion: Mastering LCM Calculations
Understanding the least common multiple is a cornerstone of mathematical proficiency. This guide has covered various methods for calculating the LCM, emphasizing the prime factorization method as the most efficient and reliable technique, especially for larger numbers. Remember, the correct LCM of 4, 6, and 3 is 12, not 72, as shown by the prime factorization method. The application of the GCD method to three or more numbers needs to be approached carefully, to avoid potentially erroneous results. By mastering these techniques, you can confidently tackle various mathematical problems involving LCM and appreciate its real-world applications. From scheduling to fraction simplification, the LCM provides a powerful tool for solving diverse problems across various disciplines.
Latest Posts
Latest Posts
-
How To Write 1500 In Words
May 12, 2025
-
Place Value Worksheets Grade 4 Pdf
May 12, 2025
-
Which Of The Following Is Not A Hindbrain Structure
May 12, 2025
-
How Many Electrons Are Shared In A Double Covalent Bond
May 12, 2025
-
Is B2 Diamagnetic Or Paramagnetic Why
May 12, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 4 6 And 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.