Lcm Of 3 6 And 7
Juapaving
Apr 08, 2025 · 5 min read
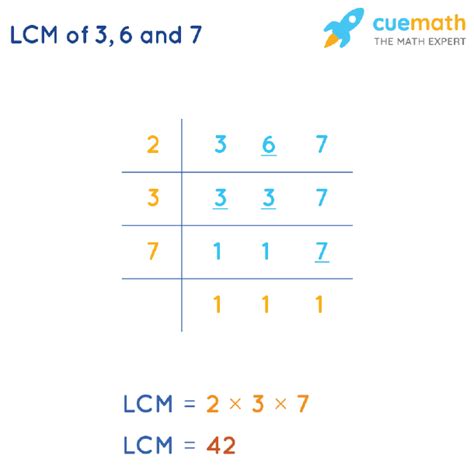
Table of Contents
Finding the Least Common Multiple (LCM) of 3, 6, and 7: A Comprehensive Guide
Finding the least common multiple (LCM) is a fundamental concept in mathematics with wide-ranging applications, from scheduling to simplifying fractions. This comprehensive guide will delve into the methods of calculating the LCM of 3, 6, and 7, exploring different approaches and providing a solid understanding of the underlying principles. We'll also look at real-world examples and explore how this seemingly simple concept plays a significant role in more advanced mathematical operations.
Understanding Least Common Multiples (LCM)
Before we jump into calculating the LCM of 3, 6, and 7, let's establish a clear understanding of what an LCM actually is. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. In simpler terms, it's the smallest number that all the given numbers can divide into evenly.
For example, let's consider the numbers 2 and 3. The multiples of 2 are 2, 4, 6, 8, 10, 12... and the multiples of 3 are 3, 6, 9, 12, 15... The common multiples of 2 and 3 are 6, 12, 18... The smallest of these common multiples is 6, hence the LCM of 2 and 3 is 6.
Methods for Calculating the LCM
Several methods exist for calculating the LCM, each with its advantages and disadvantages. Let's explore the most common approaches, focusing on their application to finding the LCM of 3, 6, and 7.
1. Listing Multiples Method
This is the most straightforward method, particularly useful for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 36, 42...
- Multiples of 6: 6, 12, 18, 24, 30, 36, 42...
- Multiples of 7: 7, 14, 21, 28, 35, 42...
By comparing the lists, we can see that the smallest common multiple of 3, 6, and 7 is 42. This method is simple but becomes less efficient as the numbers get larger.
2. Prime Factorization Method
This method is more efficient for larger numbers and provides a deeper understanding of the concept. It involves breaking down each number into its prime factors. Prime factorization is the process of expressing a number as a product of its prime numbers (numbers divisible only by 1 and themselves).
- Prime factorization of 3: 3 (3 is a prime number)
- Prime factorization of 6: 2 x 3
- Prime factorization of 7: 7 (7 is a prime number)
Once we have the prime factorization, we identify the highest power of each prime factor present in the factorizations.
- Highest power of 2: 2¹ = 2
- Highest power of 3: 3¹ = 3
- Highest power of 7: 7¹ = 7
The LCM is then calculated by multiplying these highest powers together: 2 x 3 x 7 = 42. This method is more systematic and efficient, especially when dealing with larger numbers or a greater number of integers.
3. Greatest Common Divisor (GCD) Method
The LCM and GCD (Greatest Common Divisor) are closely related. There's a formula that connects them:
LCM(a, b) x GCD(a, b) = a x b
This formula can be extended to more than two numbers. However, applying this method directly to find the LCM of 3, 6, and 7 might be less efficient than prime factorization in this specific case. Let's illustrate how it works for two numbers first and then explain the limitations when extending to more than two.
For two numbers, like 6 and 7, we first find their GCD. The GCD of 6 and 7 is 1 (they share no common factors other than 1). Then:
LCM(6, 7) = (6 x 7) / GCD(6,7) = 42 / 1 = 42
Extending this to three numbers requires multiple applications of the formula, which can make the calculation more complex. For the numbers 3, 6, and 7, it would be more efficient to use the prime factorization method.
Real-World Applications of LCM
The concept of LCM finds practical applications in various scenarios:
-
Scheduling: Imagine you have two events that happen at regular intervals. Event A happens every 3 days, and Event B happens every 6 days. To find out when both events will occur on the same day, you'd find the LCM of 3 and 6, which is 6. Therefore, both events will occur simultaneously every 6 days. Adding a third event with a cycle of 7 days would require the LCM of 3, 6, and 7, which is 42 days.
-
Fraction Simplification: When adding or subtracting fractions, finding the LCM of the denominators is crucial for finding a common denominator.
-
Gear Ratios: In mechanics, LCM is used to determine gear ratios and synchronized rotations.
-
Music Theory: LCM plays a role in understanding musical intervals and harmonic relationships.
-
Project Management: Identifying the shortest time frame for completing tasks with different durations.
Why Understanding LCM is Important
Mastering the concept of LCM is not just about solving math problems; it's about developing a crucial skill for problem-solving. The ability to identify patterns, find common factors, and apply systematic approaches are transferable skills that extend beyond mathematics. A strong understanding of LCM enhances critical thinking and analytical abilities, making it a valuable asset in various fields.
Further Exploration
This exploration of the LCM of 3, 6, and 7 provides a foundation for understanding this fundamental mathematical concept. Further exploration could include exploring different algorithms for finding LCMs, analyzing the complexity of different methods, and delving into the mathematical properties that connect LCM and GCD. The ability to efficiently compute LCMs is a stepping stone to more advanced mathematical concepts and practical applications. Understanding this seemingly simple concept opens doors to a wider understanding of number theory and its practical implications in various fields. This knowledge is essential for anyone seeking to improve their mathematical skills and problem-solving capabilities. The applications are vast, from scheduling and project management to more complex areas like computer science and engineering. The foundation of these applications lies in the simple yet powerful concept of the Least Common Multiple.
Latest Posts
Latest Posts
-
What Is A Multiple Of 17
Apr 08, 2025
-
Lines That Belong To The Same Plane And Never Intersect
Apr 08, 2025
-
220 Inches Eaquels How Many Feet
Apr 08, 2025
-
Which Expression Is Equivalent To Assume
Apr 08, 2025
-
Which Of The Following Is An Oxidation Reaction
Apr 08, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 3 6 And 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.