Lcm Of 3 5 And 9
Juapaving
May 10, 2025 · 4 min read
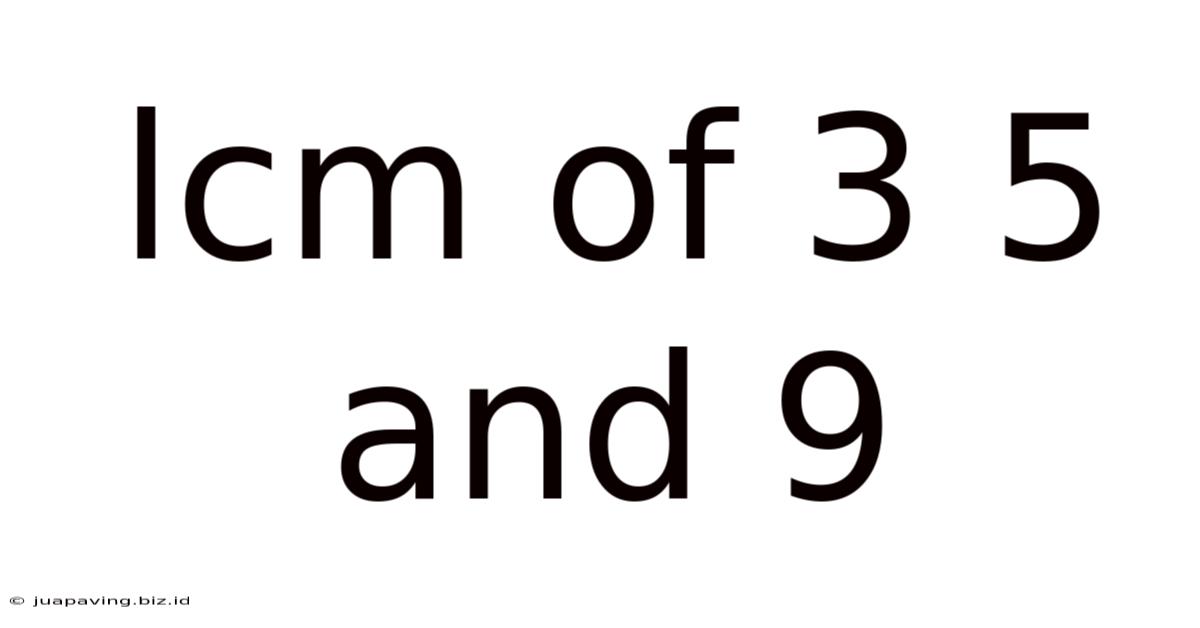
Table of Contents
Finding the LCM of 3, 5, and 9: A Comprehensive Guide
Finding the Least Common Multiple (LCM) is a fundamental concept in arithmetic and number theory, crucial for various mathematical operations and real-world applications. This article delves deep into calculating the LCM of 3, 5, and 9, exploring multiple methods and showcasing the underlying principles. We'll also touch upon the broader significance of LCMs and their uses in diverse fields.
Understanding Least Common Multiples (LCMs)
Before tackling the specific problem of finding the LCM of 3, 5, and 9, let's establish a solid understanding of what LCMs represent. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the given integers without leaving a remainder. This concept is crucial in simplifying fractions, solving problems involving cycles or repetitions, and understanding rhythmic patterns.
Key Characteristics of LCMs:
- Smallest Multiple: The LCM is always the smallest positive integer that satisfies the divisibility condition.
- Divisibility: All the given numbers must divide the LCM without leaving a remainder.
- Relevance: LCMs have practical applications in various areas, including scheduling, music, and engineering.
Methods for Calculating the LCM of 3, 5, and 9
Several methods can efficiently compute the LCM of 3, 5, and 9. We will explore three common approaches:
1. Listing Multiples Method
This method is straightforward, particularly for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, ...
- Multiples of 5: 5, 10, 15, 20, 25, 30, 35, ...
- Multiples of 9: 9, 18, 27, 36, 45, ...
By examining the lists, we observe that the smallest multiple common to all three numbers is 45. Therefore, the LCM(3, 5, 9) = 45.
This method is simple for small numbers but becomes cumbersome and inefficient for larger numbers.
2. Prime Factorization Method
This method is more efficient for larger numbers and provides a systematic approach. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of all prime factors present.
- Prime factorization of 3: 3 = 3¹
- Prime factorization of 5: 5 = 5¹
- Prime factorization of 9: 9 = 3²
To find the LCM, we take the highest power of each prime factor present in the factorizations:
- Highest power of 3: 3² = 9
- Highest power of 5: 5¹ = 5
Multiplying these highest powers together: 9 * 5 = 45
Therefore, the LCM(3, 5, 9) = 45.
This method is more efficient and scalable, especially when dealing with larger numbers.
3. Greatest Common Divisor (GCD) Method
The LCM and GCD (Greatest Common Divisor) of a set of numbers are related through the following formula:
LCM(a, b) * GCD(a, b) = a * b
This relationship can be extended to more than two numbers. While this method is less intuitive for directly calculating the LCM, it demonstrates the connection between LCM and GCD. We first find the GCD of 3, 5, and 9 using the Euclidean algorithm or prime factorization. The GCD(3, 5, 9) = 1 (as 3, 5, and 9 share no common factors other than 1).
Let's use the formula for three numbers (although a direct extension of the two-number formula is less straightforward and requires careful consideration of common factors):
LCM(3, 5, 9) = (3 * 5 * 9) / GCD(3, 5, 9) = (135) / 1 = 45
Applications of LCMs
The concept of LCM finds widespread applications in various fields:
1. Scheduling and Time Management:
Imagine you have three events that repeat at different intervals: one every 3 days, one every 5 days, and one every 9 days. To determine when all three events will coincide, you need to find the LCM(3, 5, 9) = 45. This means all three events will occur together every 45 days.
2. Music and Rhythm:
LCMs are essential in music theory for determining the least common multiple of note durations or rhythmic patterns. It helps in understanding how different rhythms can synchronize.
3. Engineering and Manufacturing:
In engineering and manufacturing, LCM is used in calculating gear ratios, synchronizing machinery, and coordinating production cycles.
4. Fraction Simplification:
Finding the LCM of the denominators is crucial when adding or subtracting fractions. It enables us to find a common denominator and simplify the calculation.
5. Modular Arithmetic:
LCM plays a role in modular arithmetic, a branch of number theory with applications in cryptography and computer science.
Conclusion: The Significance of LCM(3, 5, 9) = 45
This in-depth exploration of finding the LCM of 3, 5, and 9 has not only provided the solution (45) but also highlighted the fundamental nature of LCMs and their diverse applications. Understanding the different methods for calculating LCMs — listing multiples, prime factorization, and the GCD method — empowers you to tackle similar problems with varying complexities. The seemingly simple task of finding the LCM of three numbers underscores the interconnectedness of mathematical concepts and their practical relevance in various aspects of life. The value of 45, as the LCM of 3, 5, and 9, is not merely a numerical result; it is a keystone in understanding fundamental mathematical relationships and solving real-world problems. This understanding forms a solid foundation for further explorations in mathematics and its numerous applications.
Latest Posts
Latest Posts
-
What Happens To Air When Heated
May 10, 2025
-
Electric Field Due To Charged Disk
May 10, 2025
-
What Is A Product Of Numbers
May 10, 2025
-
Greatest Common Factor Of 20 And 8
May 10, 2025
-
Is Alcohol A Homogeneous Or Heterogeneous Mixture
May 10, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 3 5 And 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.