Lcm Of 2 And 3 And 6
Juapaving
Apr 01, 2025 · 5 min read
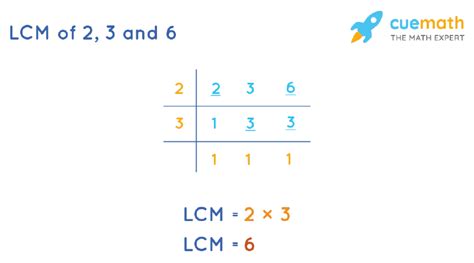
Table of Contents
Understanding the Least Common Multiple (LCM) of 2, 3, and 6
The concept of the Least Common Multiple (LCM) is fundamental in mathematics, particularly in areas like algebra, number theory, and even practical applications involving fractions and scheduling. This article delves deep into understanding the LCM, focusing specifically on the LCM of 2, 3, and 6, and exploring different methods to calculate it. We'll also examine the broader implications of LCM and its significance in various mathematical contexts.
What is the Least Common Multiple (LCM)?
The Least Common Multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that contains all the given numbers as factors. For instance, the LCM of 4 and 6 is 12 because 12 is the smallest number that is divisible by both 4 and 6.
Key Characteristics of the LCM:
- Positive Integer: The LCM is always a positive integer.
- Smallest Multiple: It's the smallest number that satisfies the divisibility condition.
- Divisibility: All the given integers must divide the LCM without leaving a remainder.
Calculating the LCM of 2, 3, and 6
Let's focus on finding the LCM of 2, 3, and 6. We can employ several methods:
Method 1: Listing Multiples
This method involves listing the multiples of each number until we find the smallest common multiple.
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20...
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21...
- Multiples of 6: 6, 12, 18, 24...
By comparing the lists, we observe that the smallest common multiple is 6. Therefore, the LCM(2, 3, 6) = 6.
Method 2: Prime Factorization
Prime factorization is a powerful technique for finding the LCM. It involves expressing each number as a product of its prime factors.
- Prime factorization of 2: 2
- Prime factorization of 3: 3
- Prime factorization of 6: 2 x 3
To find the LCM using prime factorization, we take the highest power of each prime factor present in the factorizations. In this case, we have:
- Highest power of 2: 2¹ = 2
- Highest power of 3: 3¹ = 3
Therefore, LCM(2, 3, 6) = 2 x 3 = 6. This method is particularly useful when dealing with larger numbers.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and the Greatest Common Divisor (GCD) are closely related. The relationship between the LCM and GCD of two numbers a and b is given by:
LCM(a, b) * GCD(a, b) = a * b
While this formula is primarily used for two numbers, we can extend the concept. First, let's find the LCM of 2 and 3.
- GCD(2, 3) = 1 (as 2 and 3 share no common factors other than 1)
- LCM(2, 3) * GCD(2, 3) = 2 * 3
- LCM(2, 3) * 1 = 6
- LCM(2, 3) = 6
Now, let's find the LCM of 6 and the result (6). Since they are the same number, the LCM is simply 6. Therefore, LCM(2, 3, 6) = 6.
Why is the LCM Important?
The LCM has numerous applications across various fields:
1. Fraction Operations: Finding a Common Denominator
When adding or subtracting fractions with different denominators, finding the LCM of the denominators is crucial for finding a common denominator. This allows us to perform the addition or subtraction easily.
For example, to add 1/2 and 1/3, we find the LCM of 2 and 3, which is 6. We then rewrite the fractions with a denominator of 6:
1/2 = 3/6 1/3 = 2/6
Now, we can add them: 3/6 + 2/6 = 5/6
2. Scheduling Problems: Finding the Next Occurrence
The LCM is useful in solving scheduling problems. Imagine two buses that depart from the same station, one every 2 hours and the other every 3 hours. The LCM of 2 and 3 (which is 6) represents the time it takes for both buses to depart simultaneously again.
3. Number Theory and Modular Arithmetic
The LCM plays a vital role in number theory and modular arithmetic. It's used in solving congruence problems and in determining the period of repeating decimal expansions of fractions.
4. Music Theory: Finding Harmonious Intervals
In music theory, the LCM is used to determine the least common multiple of the frequencies of different notes, which helps in determining harmonious intervals.
5. Computer Science and Algorithm Design
In computer science, the LCM is used in algorithms related to scheduling, synchronization, and data structures.
Exploring the Relationship Between 2, 3, and 6
The numbers 2, 3, and 6 are closely related. Notice that:
- 6 is a multiple of both 2 and 3.
- 2 and 3 are prime numbers, meaning they are only divisible by 1 and themselves.
- 6 is a composite number, meaning it has more than two factors (1, 2, 3, and 6).
This relationship explains why the LCM of 2, 3, and 6 is simply 6. Since 6 is already a multiple of both 2 and 3, it becomes the smallest common multiple.
Advanced Concepts and Further Exploration
While the LCM of 2, 3, and 6 is straightforward, calculating the LCM for larger sets of numbers or numbers with many factors can become more complex. Exploring advanced techniques like the Euclidean algorithm for finding the GCD and its connection to the LCM would enhance your understanding further. Furthermore, delving into the mathematical properties of the LCM and its applications in abstract algebra and number theory opens up fascinating avenues for exploration. Understanding the LCM's role in modular arithmetic and cryptography reveals its importance in modern computer science.
Conclusion
The Least Common Multiple is a fundamental concept with practical applications spanning numerous fields. Understanding its calculation methods and significance is essential for success in mathematics and related disciplines. This article has explored the LCM of 2, 3, and 6 in detail, providing various methods for its calculation and highlighting the broader importance of the LCM in mathematics and beyond. The seemingly simple calculation of the LCM of these three numbers serves as a gateway to understanding more complex mathematical concepts and their real-world applications. Continued exploration of this concept will undoubtedly deepen your mathematical understanding and problem-solving skills.
Latest Posts
Latest Posts
-
Where In A Plant Cell Does Photosynthesis Occur
Apr 02, 2025
-
A Motor And A Generator Are
Apr 02, 2025
-
Allows Materials In And Out Of The Cell
Apr 02, 2025
-
Which Of The Following Is Matched Correctly
Apr 02, 2025
-
Transitional Tissue Is Found In What System
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 2 And 3 And 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
