Lcm Of 10 15 And 25
Juapaving
May 11, 2025 · 5 min read
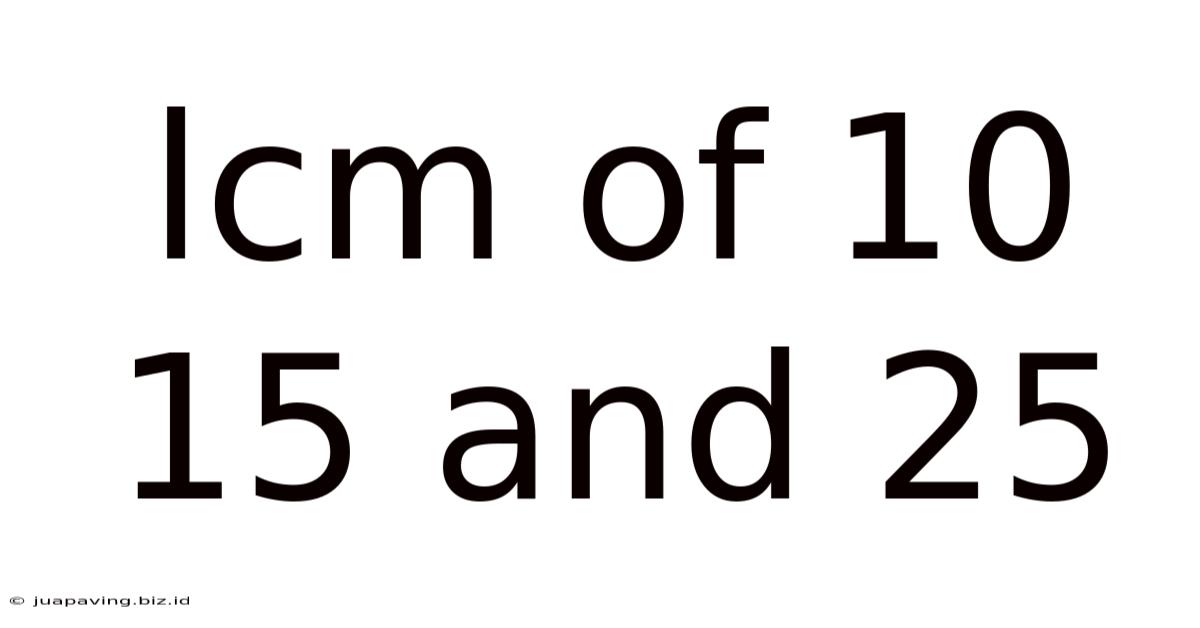
Table of Contents
Finding the LCM of 10, 15, and 25: A Comprehensive Guide
Finding the least common multiple (LCM) of numbers is a fundamental concept in mathematics with applications ranging from simple arithmetic to complex scheduling problems and even musical theory. This comprehensive guide will delve into the methods of calculating the LCM of 10, 15, and 25, exploring different approaches and highlighting the underlying mathematical principles. We'll also examine why understanding LCM is crucial and its broader relevance in various fields.
Understanding Least Common Multiple (LCM)
Before we dive into calculating the LCM of 10, 15, and 25, let's solidify our understanding of what LCM actually means. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. Think of it as the smallest number that contains all the given numbers as factors.
For example, consider the numbers 2 and 3. Their multiples are:
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20…
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30…
The common multiples of 2 and 3 are 6, 12, 18, 24, 30, and so on. The smallest of these common multiples is 6, therefore, the LCM(2, 3) = 6.
Method 1: Listing Multiples
This is the most straightforward method, especially for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
Let's find the LCM of 10, 15, and 25 using this method:
- Multiples of 10: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 150, 200, 250, 300...
- Multiples of 15: 15, 30, 45, 60, 75, 90, 105, 120, 135, 150, 165, 180, 195, 210, 225, 240, 255, 270, 285, 300...
- Multiples of 25: 25, 50, 75, 100, 125, 150, 175, 200, 225, 250, 275, 300...
By comparing the lists, we can see that the smallest common multiple is 150. Therefore, LCM(10, 15, 25) = 150.
Method 2: Prime Factorization
This method is more efficient, especially for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of all the prime factors involved.
Let's apply this method to find the LCM of 10, 15, and 25:
-
Prime Factorization:
- 10 = 2 × 5
- 15 = 3 × 5
- 25 = 5 × 5 = 5²
-
Identify the highest power of each prime factor:
- The prime factors are 2, 3, and 5.
- The highest power of 2 is 2¹ = 2.
- The highest power of 3 is 3¹ = 3.
- The highest power of 5 is 5² = 25.
-
Multiply the highest powers together:
- LCM(10, 15, 25) = 2 × 3 × 25 = 150
Therefore, the LCM of 10, 15, and 25 is 150 using the prime factorization method.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and GCD (Greatest Common Divisor) are closely related. There's a formula that connects them:
LCM(a, b) × GCD(a, b) = a × b
This formula can be extended to more than two numbers, although the calculation becomes more complex. For three numbers, it's less straightforward and generally less efficient than prime factorization, particularly for larger numbers. However, let's illustrate the concept:
First, we need to find the GCD of 10, 15, and 25. The GCD is the largest number that divides all three numbers without leaving a remainder. In this case, the GCD(10, 15, 25) = 5.
While the direct application of the LCM * GCD formula is cumbersome for three or more numbers, the concept highlights the inherent relationship between LCM and GCD. The prime factorization method remains the most practical for efficiently calculating the LCM of multiple numbers.
Real-World Applications of LCM
Understanding LCM isn't just about solving math problems; it has significant practical applications in various fields:
-
Scheduling: Imagine you have three machines that complete cycles in 10, 15, and 25 minutes respectively. To find when they'll all complete a cycle simultaneously, you need the LCM. The LCM (150 minutes) represents the time they'll all finish together.
-
Music: Musical rhythms and harmonies often rely on LCM calculations. Determining when different rhythmic patterns will coincide involves finding the LCM of their durations.
-
Construction and Engineering: In projects involving repetitive tasks or synchronized movements (like conveyor belts or gears), calculating LCM is essential for efficient design and operation.
Why is Understanding LCM Important?
Mastering the concept of LCM builds a strong foundation in number theory and problem-solving. Its applications extend beyond basic arithmetic, revealing its importance in various practical scenarios. Being able to efficiently calculate LCM demonstrates a strong grasp of fundamental mathematical principles and enhances analytical skills. It’s a crucial skill that transcends the classroom and finds relevance in numerous real-world applications.
Conclusion
Finding the LCM of 10, 15, and 25, whether through listing multiples, prime factorization, or understanding its relationship with GCD, showcases different approaches to solving the same problem. The prime factorization method proves to be the most efficient and adaptable approach, particularly when dealing with larger numbers or more variables. The importance of LCM lies not only in its mathematical significance but also in its practical applications across various disciplines. A solid understanding of LCM enhances problem-solving abilities and provides a valuable tool for tackling complex real-world situations. By grasping these concepts, you’re not only improving your mathematical understanding but also equipping yourself with a valuable skill set for numerous applications.
Latest Posts
Latest Posts
-
Can Animals Make Their Own Food
May 13, 2025
-
What Happens In A Flower After Fertilization
May 13, 2025
-
What Type Of Epithelium Lines The Kidney Tubules
May 13, 2025
-
Is Baking Soda Acid Base Or Neutral
May 13, 2025
-
Five Letter Words With E R
May 13, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 10 15 And 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.