Is The Square Root Of 50 Rational Or Irrational
Juapaving
Mar 29, 2025 · 5 min read
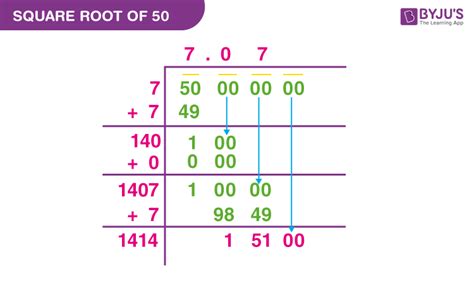
Table of Contents
Is the Square Root of 50 Rational or Irrational? A Deep Dive into Number Theory
The question of whether the square root of 50 is rational or irrational might seem simple at first glance. However, understanding the answer requires delving into the fundamental concepts of number theory, specifically the definitions of rational and irrational numbers, and the properties of perfect squares. This article will not only answer the question definitively but also explore the broader context, providing a solid foundation for understanding similar problems.
Understanding Rational and Irrational Numbers
Before tackling the square root of 50, let's establish a clear understanding of the terminology.
Rational Numbers: A rational number is any number that can be expressed as a fraction p/q, where p and q are integers, and q is not equal to zero. Examples include 1/2, 3/4, -2/5, and even whole numbers like 5 (which can be written as 5/1). The key characteristic is the ability to represent the number as a ratio of two integers. When expressed as decimals, rational numbers either terminate (e.g., 0.75) or repeat in a predictable pattern (e.g., 0.333...).
Irrational Numbers: Irrational numbers cannot be expressed as a simple fraction of two integers. Their decimal representations are non-terminating and non-repeating. Famous examples include π (pi), approximately 3.14159..., and e (Euler's number), approximately 2.71828.... The square root of most non-perfect squares is also irrational.
Perfect Squares and Their Square Roots
A perfect square is a number that can be obtained by squaring an integer. For example, 9 is a perfect square because 3² = 9. The square root of a perfect square is always an integer. Conversely, the square root of a number that is not a perfect square will always be irrational. This is a crucial point in determining the nature of √50.
Determining the Nature of √50
To determine if √50 is rational or irrational, we need to investigate whether 50 is a perfect square. Let's examine the integers and their squares:
- 1² = 1
- 2² = 4
- 3² = 9
- 4² = 16
- 5² = 25
- 6² = 36
- 7² = 49
- 8² = 64
As we can see, 50 falls between 7² (49) and 8² (64). It is not a perfect square. Therefore, its square root, √50, cannot be expressed as a fraction of two integers. This definitively concludes that √50 is an irrational number.
Simplifying Irrational Numbers: The Role of Prime Factorization
While √50 is irrational, we can simplify it to a certain extent. This involves prime factorization:
50 = 2 x 5 x 5 = 2 x 5²
Therefore, √50 = √(2 x 5²) = √2 x √5² = 5√2
This simplified form, 5√2, is still irrational because √2 is irrational. The multiplication of a rational number (5) by an irrational number (√2) results in an irrational number.
Further Exploration: Proof by Contradiction
We can rigorously prove the irrationality of √50 (and indeed, the square root of any non-perfect square) using a proof by contradiction.
1. Assumption: Let's assume, for the sake of contradiction, that √50 is rational. This means it can be expressed as a fraction p/q, where p and q are integers, q ≠ 0, and p and q are in their simplest form (meaning they share no common factors other than 1).
2. Equation: If √50 = p/q, then squaring both sides gives us 50 = p²/q².
3. Rearrangement: This can be rearranged to 50q² = p².
4. Divisibility by 2 and 5: This equation shows that p² is divisible by both 2 and 5 (since 50 = 2 x 5²). If p² is divisible by 2, then p must also be divisible by 2 (because the square of an odd number is odd, and the square of an even number is even). Similarly, if p² is divisible by 5, then p must also be divisible by 5.
5. Rewriting p: Therefore, we can rewrite p as 2 x 5 x k = 10k, where k is another integer.
6. Substitution and Simplification: Substituting this into the equation 50q² = p², we get:
50q² = (10k)² 50q² = 100k² q² = 2k²
7. Contradiction: This equation shows that q² is divisible by 2, and therefore q must also be divisible by 2.
8. Conclusion: We've now shown that both p and q are divisible by 2, contradicting our initial assumption that p/q is in its simplest form. This contradiction means our initial assumption (that √50 is rational) must be false. Therefore, √50 is irrational.
Practical Applications and Real-World Relevance
While the concept of irrational numbers might seem purely theoretical, they have significant practical applications:
- Geometry: Irrational numbers frequently appear in geometric calculations, particularly when dealing with circles (using π) and diagonals of squares (involving √2).
- Physics: Many physical phenomena involve irrational numbers in their mathematical descriptions.
- Engineering: Precise engineering calculations often require the use of irrational numbers for accuracy.
Understanding the distinction between rational and irrational numbers is fundamental to advanced mathematics and its applications in various scientific and engineering disciplines.
Conclusion
The square root of 50 is undeniably irrational. This conclusion stems directly from the fact that 50 is not a perfect square, and a more rigorous proof by contradiction further solidifies this understanding. This exploration provides a solid foundation for comprehending the nature of square roots and the broader classification of numbers within number theory. The concepts discussed here are not just abstract mathematical ideas; they have profound implications for various fields, highlighting the importance of understanding the properties of rational and irrational numbers. Furthermore, the ability to simplify irrational numbers, as demonstrated with 5√2, provides practical value in mathematical calculations.
Latest Posts
Latest Posts
-
Coordination Of Balance And Body Movement Is Controlled By The
Mar 31, 2025
-
Why Are The Cells Generally Of A Small Size
Mar 31, 2025
-
Is Calcium Hydroxide A Base Or Acid
Mar 31, 2025
-
The Ultimate Source Of Energy From Fossil Fuels Is The
Mar 31, 2025
-
Dna Is A Polymer Made From What Monomer Units
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about Is The Square Root Of 50 Rational Or Irrational . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
