Is The Square Root Of 12 A Rational Number
Juapaving
Mar 21, 2025 · 4 min read
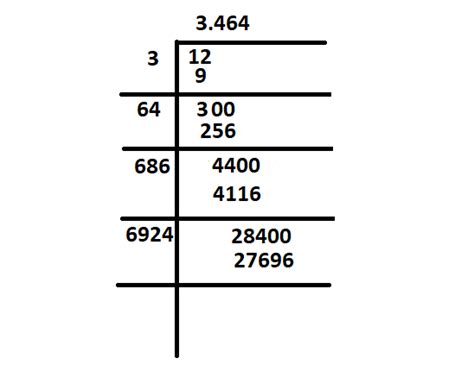
Table of Contents
Is the Square Root of 12 a Rational Number? A Deep Dive into Irrationality
The question of whether the square root of 12 is a rational number is a fundamental one in mathematics, touching upon the core concepts of rational and irrational numbers. Understanding this requires a solid grasp of these definitions and the properties of numbers. This article will explore the question comprehensively, providing a detailed explanation and delving into the broader implications.
Understanding Rational and Irrational Numbers
Before we tackle the square root of 12, let's establish a clear understanding of rational and irrational numbers.
Rational Numbers: A rational number is any number that can be expressed as a fraction p/q, where p and q are integers, and q is not equal to zero. Examples include 1/2, 3/4, -2/5, and even whole numbers like 5 (which can be expressed as 5/1). The decimal representation of a rational number either terminates (e.g., 0.75) or repeats in a predictable pattern (e.g., 0.333...).
Irrational Numbers: Irrational numbers, conversely, cannot be expressed as a fraction of two integers. Their decimal representations are non-terminating and non-repeating. Famous examples include pi (π) and the square root of 2 (√2). These numbers continue infinitely without ever settling into a repeating pattern.
Exploring the Square Root of 12
Now, let's examine the square root of 12 (√12). To determine if it's rational or irrational, we need to try and express it as a fraction p/q. Let's begin by simplifying the square root:
√12 = √(4 * 3) = √4 * √3 = 2√3
This simplification shows that √12 is equivalent to 2 multiplied by the square root of 3. The key here is the √3 component. Can we express √3 as a fraction p/q?
Proof by Contradiction: Demonstrating the Irrationality of √3
To definitively prove that √3 is irrational (and therefore √12 is also irrational), we'll use a classic mathematical technique called proof by contradiction.
-
Assumption: Let's assume, for the sake of contradiction, that √3 is rational. This means it can be expressed as a fraction p/q, where p and q are integers, q ≠ 0, and the fraction is in its simplest form (meaning p and q share no common factors other than 1).
-
Squaring Both Sides: If √3 = p/q, then squaring both sides gives us: 3 = p²/q²
-
Rearrangement: We can rearrange this equation to: 3q² = p²
-
Deduction: This equation tells us that p² is a multiple of 3. Since 3 is a prime number, this implies that p itself must also be a multiple of 3. We can express this as p = 3k, where k is another integer.
-
Substitution: Substituting p = 3k back into the equation 3q² = p², we get: 3q² = (3k)² = 9k²
-
Simplification: Dividing both sides by 3, we arrive at: q² = 3k²
-
Another Deduction: This equation shows that q² is also a multiple of 3, which means q itself must be a multiple of 3.
-
Contradiction: We've now shown that both p and q are multiples of 3. This contradicts our initial assumption that p/q was in its simplest form (they share no common factors). This contradiction proves our initial assumption was false.
-
Conclusion: Therefore, √3 cannot be expressed as a fraction p/q, meaning it is irrational. Since √12 = 2√3, and 2 multiplied by an irrational number remains irrational, √12 is also an irrational number.
Implications and Further Exploration
The irrationality of √12 has several significant implications:
-
Incommensurability: It demonstrates the existence of incommensurable magnitudes. This means there's no common unit of measurement that can perfectly divide both a line segment of length 1 and a line segment of length √12. This concept was a significant discovery in ancient Greek mathematics.
-
Decimal Representation: The decimal representation of √12 is a non-terminating, non-repeating decimal. You can approximate it (approximately 3.464), but you can never express its exact value using a finite number of digits.
-
Geometric Constructions: The fact that √12 is irrational has implications for geometric constructions using only a compass and straightedge. Certain lengths and shapes cannot be perfectly constructed using these tools due to the involvement of irrational numbers.
-
Applications in Advanced Mathematics: Irrational numbers play a crucial role in advanced mathematical fields like calculus, analysis, and number theory. They form the basis for many important theorems and concepts.
Beyond √12: Identifying Other Irrational Numbers
The method of proof by contradiction used to show the irrationality of √3 can be adapted to prove the irrationality of many other square roots of non-perfect squares. In general, the square root of any positive integer that is not a perfect square (i.e., not the square of an integer) will be irrational.
Conclusion: The Irrational Nature of √12
In conclusion, the square root of 12 is definitively an irrational number. This understanding stems from a clear definition of rational and irrational numbers and is rigorously proven through the method of proof by contradiction. The irrationality of √12, and irrational numbers in general, highlights a fascinating aspect of mathematics – the existence of numbers that defy simple fractional representation, yet play a fundamental role in shaping our understanding of the mathematical world. The exploration of such concepts deepens our appreciation for the intricacies and beauty of mathematics.
Latest Posts
Latest Posts
-
Solid Has A Definite Shape And Volume
Mar 27, 2025
-
What Is The Percentage Of 32 Out Of 40
Mar 27, 2025
-
Words With Ie In Them 5 Letters
Mar 27, 2025
-
What Are The Pros Of Fossil Fuels
Mar 27, 2025
-
An Object Following A Straight Line Path At Constant Speed
Mar 27, 2025
Related Post
Thank you for visiting our website which covers about Is The Square Root Of 12 A Rational Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
