Is A Parabola A One To One Function
Juapaving
Mar 27, 2025 · 6 min read
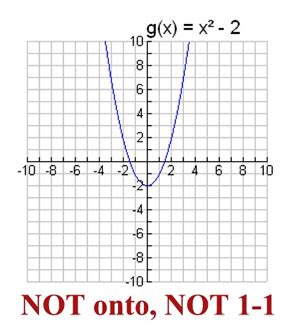
Table of Contents
Is a Parabola a One-to-One Function? Exploring the Concepts of Functions and their Inverses
The question of whether a parabola represents a one-to-one function is a fundamental concept in algebra and precalculus. Understanding this requires a solid grasp of what constitutes a function, a one-to-one function, and how the properties of parabolas relate to these definitions. This comprehensive article will delve into these concepts, providing a detailed explanation with illustrative examples.
Understanding Functions
A function is a relationship between a set of inputs (the domain) and a set of possible outputs (the codomain) with the property that each input is related to exactly one output. This is often represented using function notation, such as f(x), where x represents the input and f(x) represents the output. Graphically, a function satisfies the vertical line test: any vertical line drawn on the graph will intersect the function at most once.
Examples of Functions:
- Linear functions: f(x) = 2x + 1 (A straight line)
- Quadratic functions: f(x) = x² (A parabola)
- Exponential functions: f(x) = eˣ (An exponentially increasing curve)
Non-Examples of Functions:
A circle, for instance, fails the vertical line test. A vertical line can intersect a circle at two points, indicating that a single x-value corresponds to multiple y-values, thus violating the definition of a function.
One-to-One Functions (Injections)
A one-to-one function, also known as an injection, is a special type of function where each output value corresponds to exactly one input value. In other words, no two different inputs produce the same output. Graphically, a one-to-one function satisfies the horizontal line test: any horizontal line drawn on the graph intersects the function at most once.
Examples of One-to-One Functions:
- Linear functions (with non-zero slope): f(x) = 2x + 1
- Exponential functions: f(x) = eˣ
Non-Examples of One-to-One Functions:
- Quadratic functions: f(x) = x² (A parabola) – Notice that both x = 2 and x = -2 result in the same output, f(x) = 4.
- Absolute value functions: f(x) = |x| (A V-shaped graph) – Similar to the parabola, positive and negative x-values yield the same positive y-value.
Parabolas and the One-to-One Property
A parabola, represented by a quadratic function of the form f(x) = ax² + bx + c (where a ≠ 0), is inherently not a one-to-one function. This is due to its symmetrical nature. The parabola's vertex acts as a point of symmetry. For every y-value (except the y-coordinate of the vertex), there are two corresponding x-values that produce that y-value. This directly violates the definition of a one-to-one function.
Visualizing the Failure of the Horizontal Line Test for Parabolas
Imagine drawing a horizontal line across a parabola. If the line intersects the parabola's curve at two points, this confirms the existence of two distinct x-values that map to the same y-value. This immediately fails the horizontal line test, proving that the parabola is not a one-to-one function.
Mathematical Proof
Consider a simple parabola f(x) = x². Let's assume there exist two distinct inputs, x₁ and x₂, such that f(x₁) = f(x₂). Then:
x₁² = x₂²
Taking the square root of both sides:
x₁ = ±x₂
This equation shows that unless x₁ = x₂ = 0, there are always two distinct values of x (x₁ and x₂) that produce the same output value. This is a clear demonstration that a standard parabola is not a one-to-one function.
Restricting the Domain to Achieve One-to-One Property
While a complete parabola is not a one-to-one function, we can create a one-to-one function by restricting the domain of the parabola. By limiting the inputs to a specific interval, we can ensure that each output corresponds to only one input.
The Method of Restriction
Typically, we restrict the domain of a parabola to either its left or right half. This eliminates the symmetry and creates a function that passes the horizontal line test.
For example, consider the parabola f(x) = x². If we restrict the domain to x ≥ 0, the resulting function is one-to-one. Similarly, restricting the domain to x ≤ 0 also results in a one-to-one function. Graphically, this means considering only one branch of the parabola.
Implications of Domain Restriction
Restricting the domain is a crucial step when finding the inverse of a parabola. Since only one-to-one functions have inverses, we must restrict the domain of the original quadratic function before attempting to find its inverse.
Finding the Inverse of a Restricted Parabola
Once we have restricted the domain to create a one-to-one function, we can find its inverse function. The inverse function essentially reverses the mapping of the original function; it takes the output values and maps them back to their corresponding input values.
To find the inverse:
- Replace f(x) with y: This helps in manipulating the equation more easily.
- Swap x and y: This reflects the reversal of the mapping.
- Solve for y: This isolates y and expresses it in terms of x.
- Replace y with f⁻¹(x): This represents the inverse function.
Example: Let's find the inverse of the parabola f(x) = x², with the domain restricted to x ≥ 0.
- y = x²
- x = y²
- y = √x (We choose the positive square root since our restricted domain is x ≥ 0)
- f⁻¹(x) = √x
Therefore, the inverse of the restricted parabola is f⁻¹(x) = √x.
Conclusion: Parabolas and One-to-One Functions – A Summary
In conclusion, a standard parabola defined by a quadratic function of the form f(x) = ax² + bx + c (where a ≠ 0) is not a one-to-one function. Its inherent symmetry means that for every y-value (except the y-coordinate of the vertex), there are two corresponding x-values. However, by carefully restricting the domain of the parabola to either its left or right half, we can create a one-to-one function, making it possible to determine its inverse. This restriction is essential for various mathematical applications and demonstrates the importance of understanding function properties and their implications. The concept of one-to-one functions is crucial in many areas of mathematics and plays a significant role in calculus, particularly in dealing with inverse functions and their derivatives. Understanding these properties allows for a more profound understanding of mathematical relationships and their graphical representations.
Latest Posts
Latest Posts
-
What Is 0 07 As A Percent
Mar 30, 2025
-
Words That Start With A V
Mar 30, 2025
-
Labeling The Parts Of The Flower
Mar 30, 2025
-
When Does Lhopitals Rule Not Apply
Mar 30, 2025
-
The Push Or Pull On An Object Is Called
Mar 30, 2025
Related Post
Thank you for visiting our website which covers about Is A Parabola A One To One Function . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
