Is 7 12 Greater Than 1 2
Juapaving
May 13, 2025 · 5 min read
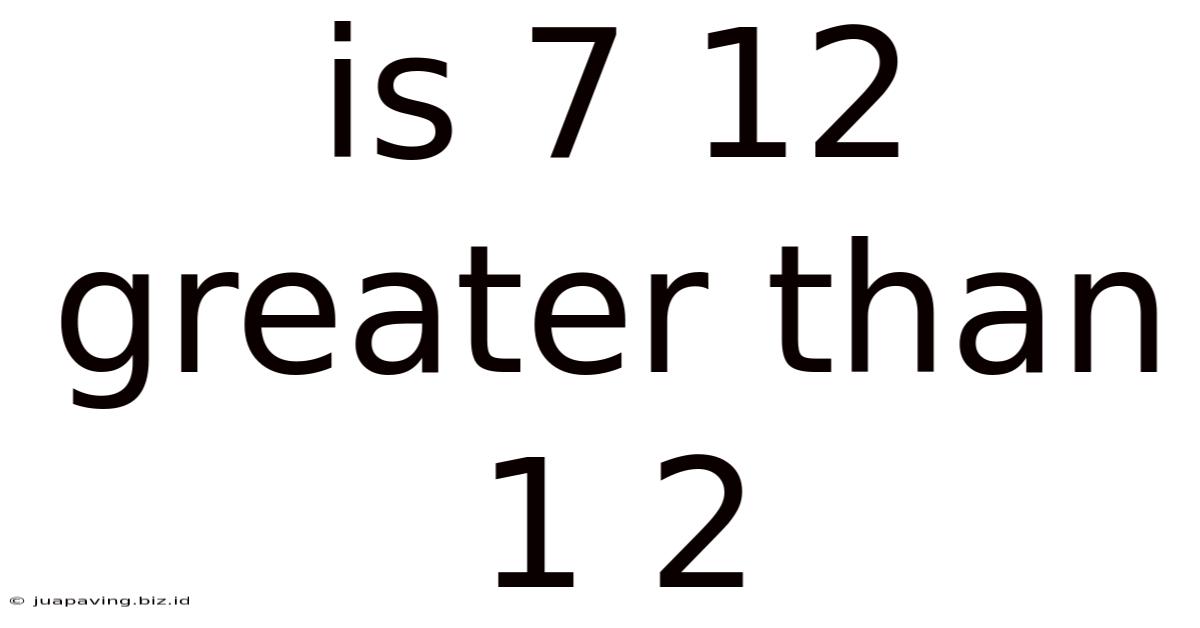
Table of Contents
Is 7/12 Greater Than 1/2? A Comprehensive Exploration of Fraction Comparison
The question, "Is 7/12 greater than 1/2?", might seem simple at first glance. However, a deeper dive into the topic reveals a wealth of mathematical concepts and practical applications relevant to understanding fractions and their comparisons. This article will not only answer the question definitively but also explore various methods for comparing fractions, providing you with the tools to tackle similar problems with confidence.
Understanding Fractions: A Quick Refresher
Before we tackle the specific problem, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates the total number of equal parts the whole is divided into, while the numerator indicates how many of those parts are being considered.
For instance, in the fraction 7/12, 12 represents the total number of equal parts, and 7 represents the number of parts we're interested in. Similarly, in the fraction 1/2, the whole is divided into two equal parts, and we're considering one of them.
Method 1: Finding a Common Denominator
One of the most common and reliable methods for comparing fractions is to find a common denominator. This means converting both fractions so they have the same denominator. Once they share a denominator, comparing the numerators directly determines which fraction is larger.
To compare 7/12 and 1/2, we need to find a common denominator for 12 and 2. The least common multiple (LCM) of 12 and 2 is 12. We already have 7/12, so we only need to convert 1/2.
To convert 1/2 to a fraction with a denominator of 12, we multiply both the numerator and the denominator by 6:
(1 × 6) / (2 × 6) = 6/12
Now we can compare 7/12 and 6/12. Since 7 > 6, we can conclude that 7/12 > 6/12, and therefore, 7/12 > 1/2.
Advantages of the Common Denominator Method:
- Simplicity and Accuracy: This method is straightforward and guarantees an accurate comparison.
- Conceptual Understanding: It reinforces the understanding of equivalent fractions and the concept of dividing a whole into equal parts.
- Wide Applicability: It works for comparing any two fractions, regardless of their complexity.
Disadvantages of the Common Denominator Method:
- Can be Time-Consuming: Finding the LCM for larger denominators can sometimes be time-consuming, especially without the use of calculators.
- Requires Fraction Manipulation: Students need to be comfortable with multiplying and dividing fractions.
Method 2: Converting to Decimals
Another effective method for comparing fractions is to convert them into decimal numbers. This involves dividing the numerator by the denominator for each fraction.
Let's convert 7/12 and 1/2 into decimals:
7 ÷ 12 ≈ 0.5833 1 ÷ 2 = 0.5
Comparing the decimal values, we see that 0.5833 > 0.5. Therefore, 7/12 > 1/2.
Advantages of the Decimal Conversion Method:
- Easy Comparison: Comparing decimal numbers is generally simpler and more intuitive than comparing fractions.
- Familiarity: Most people are comfortable working with decimal numbers.
- Use of Calculators: Calculators can quickly convert fractions to decimals, making the process efficient.
Disadvantages of the Decimal Conversion Method:
- Rounding Errors: Depending on the decimal places used, rounding errors might slightly affect the accuracy of the comparison, especially for fractions that result in non-terminating decimals.
- Loss of Exactness: Decimal representations can sometimes lose the precision inherent in fractional representations.
- Limited Conceptual Understanding: This method might not as effectively promote a deep understanding of fractions as the common denominator method.
Method 3: Visual Representation
Visual aids can be particularly helpful when comparing fractions, especially for beginners. Imagine two identical circles.
- Divide one circle into 12 equal slices and shade 7 of them. This visually represents 7/12.
- Divide the other circle into 2 equal halves and shade one half. This visually represents 1/2.
By comparing the shaded areas, it's visually apparent that the shaded area representing 7/12 is larger than the shaded area representing 1/2. This confirms that 7/12 > 1/2.
Advantages of Visual Representation:
- Intuitive Understanding: Visual methods are highly intuitive and can aid in grasping the concept of fractions.
- Effective for Beginners: This is particularly useful for students who are still developing their understanding of fractions.
- Practical Application: It connects abstract concepts to concrete representations.
Disadvantages of Visual Representation:
- Limited Accuracy: Precise visual comparisons can be challenging for complex fractions.
- Time-Consuming: Drawing accurate diagrams for larger fractions can be time-consuming.
- Not Suitable for Advanced Comparisons: This method is less practical for comparing many fractions or very complex fractions.
Method 4: Benchmark Fractions
Utilizing benchmark fractions (common fractions like 1/2, 1/4, 3/4, etc.) can provide a quick and efficient way to compare fractions. We know that 1/2 is equivalent to 6/12. Since 7/12 is greater than 6/12, it follows that 7/12 is greater than 1/2.
Advantages of Benchmark Fractions:
- Speed and Efficiency: This method is fast and requires minimal calculations.
- Mental Math: It encourages the development of mental math skills for fraction estimation.
- Intuitive Approach: It relies on familiar and easily recognizable fractions.
Disadvantages of Benchmark Fractions:
- Limited Applicability: This method works best for fractions easily compared to benchmark fractions. It's not as reliable for comparing more complex or unusual fractions.
- Requires Familiarity with Benchmarks: Effective use necessitates a strong understanding of benchmark fractions.
Conclusion: 7/12 is Indeed Greater Than 1/2
Through various methods – finding a common denominator, converting to decimals, visual representation, and using benchmark fractions – we have definitively established that 7/12 is greater than 1/2. Understanding these different approaches provides a versatile toolkit for comparing fractions in various contexts, from everyday tasks to more complex mathematical problems. Mastering these methods will significantly improve your mathematical skills and confidence in handling fractions. The choice of method often depends on personal preference, the complexity of the fractions involved, and the available resources. Remember, the key is to choose a method you understand well and can apply accurately.
Latest Posts
Latest Posts
-
Five Letter Word Ends In Ead
May 13, 2025
-
Two Main Sources Of Genetic Variation
May 13, 2025
-
Do Diagonals Of A Rhombus Bisect Each Other
May 13, 2025
-
Como Se Escribe 760 En Ingles
May 13, 2025
-
5 Letter Words Starting With I And Ending In E
May 13, 2025
Related Post
Thank you for visiting our website which covers about Is 7 12 Greater Than 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.