Is 6 10 Greater Than 1 2
Juapaving
May 13, 2025 · 4 min read
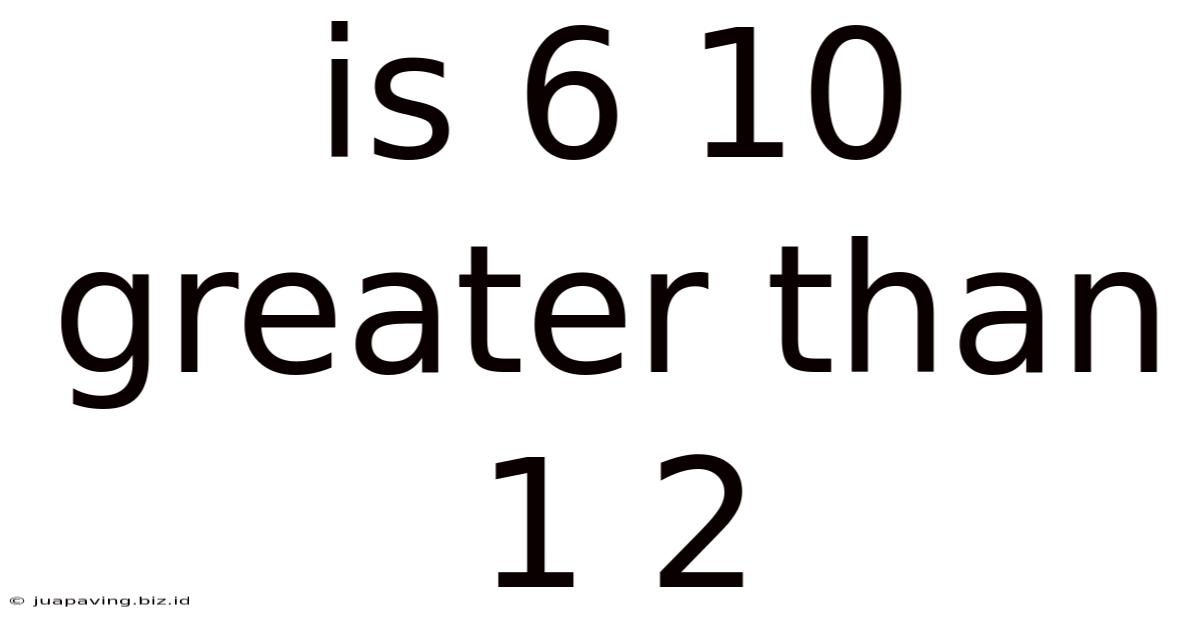
Table of Contents
Is 6/10 Greater Than 1/2? A Deep Dive into Fraction Comparison
The question, "Is 6/10 greater than 1/2?" might seem simple at first glance, particularly for those comfortable with fractions. However, a deeper exploration of this seemingly basic comparison offers a valuable opportunity to reinforce fundamental mathematical concepts and explore various approaches to solving such problems. This article will not only answer the question definitively but also delve into the methods used to compare fractions, highlighting the importance of understanding these techniques for more complex mathematical problems.
Understanding Fractions: The Building Blocks
Before tackling the comparison, let's solidify our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into.
For example, in the fraction 6/10, 6 is the numerator (the number of parts we have), and 10 is the denominator (the total number of equal parts). Similarly, in the fraction 1/2, 1 is the numerator, and 2 is the denominator.
Method 1: Converting to Decimals
One straightforward method for comparing fractions is to convert them into decimals. This involves dividing the numerator by the denominator.
- 6/10 as a decimal: 6 ÷ 10 = 0.6
- 1/2 as a decimal: 1 ÷ 2 = 0.5
Now, comparing 0.6 and 0.5 is trivial. 0.6 is greater than 0.5, therefore, 6/10 is greater than 1/2.
Method 2: Finding a Common Denominator
Another common and fundamental approach involves finding a common denominator for both fractions. A common denominator is a number that is a multiple of both denominators. This allows for a direct comparison of the numerators.
The denominators in our example are 10 and 2. A common denominator is 10 (since 10 is a multiple of both 10 and 2).
- Converting 6/10: This fraction already has a denominator of 10, so it remains 6/10.
- Converting 1/2: To get a denominator of 10, we multiply both the numerator and the denominator by 5 (because 2 x 5 = 10): (1 x 5) / (2 x 5) = 5/10
Now we compare 6/10 and 5/10. Since 6 is greater than 5, 6/10 is greater than 5/10, and consequently, 6/10 is greater than 1/2.
Method 3: Visual Representation
Visual aids can be incredibly helpful, especially for beginners. Imagine a pizza cut into 10 equal slices. 6/10 represents having 6 slices. Now imagine another pizza cut into 2 equal halves. 1/2 represents having one half. It's visually apparent that 6 out of 10 slices is more pizza than 1 out of 2 halves.
Method 4: Simplifying Fractions
Before employing any of the above methods, it’s often beneficial to simplify fractions. Simplifying involves reducing the fraction to its lowest terms by dividing both the numerator and denominator by their greatest common divisor (GCD).
In our case:
- 6/10: The GCD of 6 and 10 is 2. Dividing both by 2 gives us 3/5.
- 1/2: This fraction is already in its simplest form.
Now we can compare 3/5 and 1/2 using any of the methods described above. Converting to decimals: 3/5 = 0.6 and 1/2 = 0.5. Again, 0.6 > 0.5, confirming that 6/10 (or 3/5) is greater than 1/2.
The Importance of Fraction Comparison
Understanding how to compare fractions is crucial for a variety of reasons:
- Everyday Applications: From cooking and baking (measuring ingredients) to sharing items fairly, fraction comparison is encountered frequently in daily life.
- Advanced Mathematics: Proficiency in comparing fractions forms the foundation for understanding more complex mathematical concepts, including algebra, calculus, and beyond.
- Problem-Solving Skills: The various methods for comparing fractions enhance problem-solving skills by introducing different approaches to arriving at the same solution. This fosters critical thinking and adaptability.
Extending the Concept: Comparing More Complex Fractions
The principles discussed above can be readily extended to compare fractions with larger numbers or more complex forms. The key remains consistent: either find a common denominator, convert to decimals, or employ visual aids to aid in the comparison. Simplifying fractions before comparison often simplifies the process.
Conclusion: 6/10 Triumphs!
To reiterate, yes, 6/10 is greater than 1/2. This seemingly simple comparison serves as a potent reminder of the fundamental importance of understanding fractions and the various techniques employed to compare them effectively. Mastering these techniques is not merely about solving simple fraction problems but about developing a strong foundation for success in higher-level mathematics and various real-world applications. The methods outlined in this article provide a comprehensive toolkit for tackling fraction comparisons, regardless of their complexity. Remember to choose the method that best suits your understanding and the specific problem at hand. Practice makes perfect, so continue to engage with these concepts to build your mathematical prowess.
Latest Posts
Latest Posts
-
An Integer Divided By An Integer Is An Integer
May 13, 2025
-
What Is The Difference Between Sn1 And Sn2
May 13, 2025
-
Is Kinetic Energy A Scalar Quantity
May 13, 2025
-
Round 41 To The Nearest Ten
May 13, 2025
-
Unit Of Rate Constant For Second Order Reaction
May 13, 2025
Related Post
Thank you for visiting our website which covers about Is 6 10 Greater Than 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.