Is 3 A Multiple Of 24
Juapaving
May 12, 2025 · 5 min read
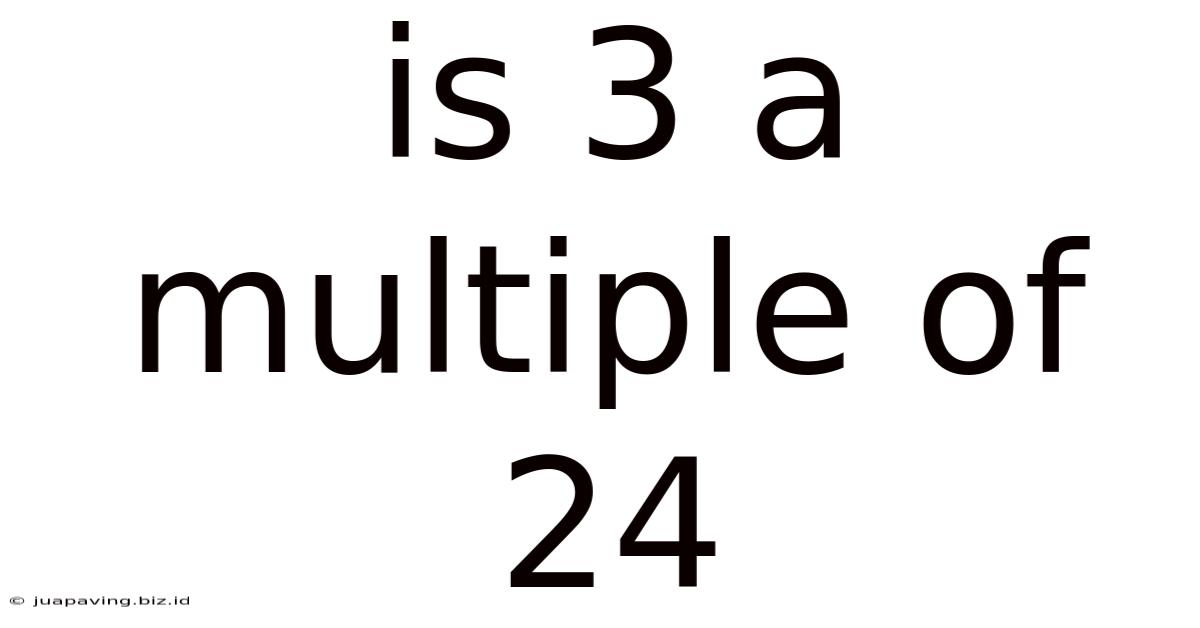
Table of Contents
Is 3 a Multiple of 24? Understanding Multiples and Divisibility
The question, "Is 3 a multiple of 24?" might seem deceptively simple, but it provides a fantastic opportunity to explore the fundamental concepts of multiples, divisibility, and number theory. The short answer is no, 3 is not a multiple of 24. However, understanding why this is the case requires a deeper dive into the mathematical definitions involved. This article will explore this concept in detail, clarifying the relationships between multiples, divisors, and factors, and providing examples to solidify your understanding.
Understanding Multiples
A multiple of a number is the product of that number and any integer (whole number). In simpler terms, it's the result of multiplying a number by another whole number. For instance:
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26... (and so on to infinity)
- Multiples of 5: 5, 10, 15, 20, 25, 30, 35... (and so on to infinity)
- Multiples of 10: 10, 20, 30, 40, 50... (and so on to infinity)
Notice that the multiples of a number continue infinitely in both positive and negative directions. However, we often focus on the positive multiples.
Identifying Multiples
To determine if a number is a multiple of another, we can perform division. If the division results in a whole number (no remainder), then the dividend is a multiple of the divisor. Let's take the example of 24:
- Is 48 a multiple of 24? 48 ÷ 24 = 2 (a whole number), so yes, 48 is a multiple of 24.
- Is 72 a multiple of 24? 72 ÷ 24 = 3 (a whole number), so yes, 72 is a multiple of 24.
- Is 3 a multiple of 24? 3 ÷ 24 = 0.125 (not a whole number), so no, 3 is not a multiple of 24.
This division method provides a clear and efficient way to test for multiples.
Understanding Divisibility
Divisibility is closely related to the concept of multiples. A number is divisible by another number if the first number can be divided by the second number without leaving a remainder. This is essentially the same as saying that the first number is a multiple of the second number.
For example:
- 24 is divisible by 2 (24 ÷ 2 = 12)
- 24 is divisible by 3 (24 ÷ 3 = 8)
- 24 is divisible by 4 (24 ÷ 4 = 6)
- 24 is divisible by 6 (24 ÷ 6 = 4)
- 24 is divisible by 8 (24 ÷ 8 = 3)
- 24 is divisible by 12 (24 ÷ 12 = 2)
- 24 is divisible by 24 (24 ÷ 24 = 1)
However, 24 is not divisible by 3, 5, 7, 9, or any number that leaves a remainder when dividing into 24.
Factors and Divisors: The Relationship
Factors and divisors are essentially interchangeable terms. They represent numbers that divide evenly into a given number. In other words, if 'a' is a factor of 'b', then 'b' is a multiple of 'a'. This reciprocal relationship is crucial to understanding multiples and divisibility.
Considering the number 24, its factors/divisors are: 1, 2, 3, 4, 6, 8, 12, and 24. Each of these numbers divides evenly into 24 without leaving a remainder.
Why 3 is Not a Multiple of 24
Returning to our original question: 3 is not a multiple of 24 because there is no integer that, when multiplied by 24, results in 3. The only way to obtain 3 from 24 is to divide 24 by 8. Division, however, does not define multiples; multiplication does.
To further illustrate this, let's consider the equation:
24 * x = 3
Solving for x, we get:
x = 3/24 = 1/8 = 0.125
Since x is not an integer, 3 cannot be a multiple of 24.
Practical Applications and Real-World Examples
Understanding multiples and divisibility is crucial in numerous fields, including:
- Measurement and Conversions: Converting units of measurement often involves working with multiples. For example, converting inches to feet (12 inches = 1 foot) requires understanding multiples of 12.
- Scheduling and Time Management: Many scheduling problems involve finding common multiples, such as determining when two events with different cycles will occur simultaneously.
- Data Organization: Divisibility and multiples are used in data structures and algorithms for efficient organization and retrieval of information.
- Pattern Recognition: Recognizing patterns in numbers often involves identifying multiples and divisibility rules.
Beyond the Basics: More Advanced Concepts
The concepts explored here form the bedrock of more advanced mathematical topics, including:
- Prime Factorization: Breaking down a number into its prime factors, which are only divisible by 1 and themselves. This helps in understanding divisibility and finding common factors.
- Greatest Common Divisor (GCD): Finding the largest number that divides evenly into two or more given numbers.
- Least Common Multiple (LCM): Finding the smallest number that is a multiple of two or more given numbers.
- Modular Arithmetic: A system of arithmetic for integers, where numbers "wrap around" upon reaching a certain value (the modulus). This is widely used in cryptography and computer science.
Understanding the fundamentals of multiples and divisibility is essential for success in mathematics and its related fields. While the question "Is 3 a multiple of 24?" initially appears simple, its exploration unveils a deeper understanding of fundamental mathematical relationships. Remember, a number is a multiple of another only if it can be obtained by multiplying the second number by an integer. Since 3 cannot be obtained by multiplying 24 by an integer, the answer remains definitively no.
Latest Posts
Latest Posts
-
Label The Structures On The Given Mitochondrion
May 12, 2025
-
What Is 17 25 As A Percent
May 12, 2025
-
What Does The Food Vacuole Do
May 12, 2025
-
Whats The Cube Root Of 8
May 12, 2025
-
Is The Smallest Unit Of Matter
May 12, 2025
Related Post
Thank you for visiting our website which covers about Is 3 A Multiple Of 24 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.