Is 3 6 Greater Than 3 8
Juapaving
May 09, 2025 · 5 min read
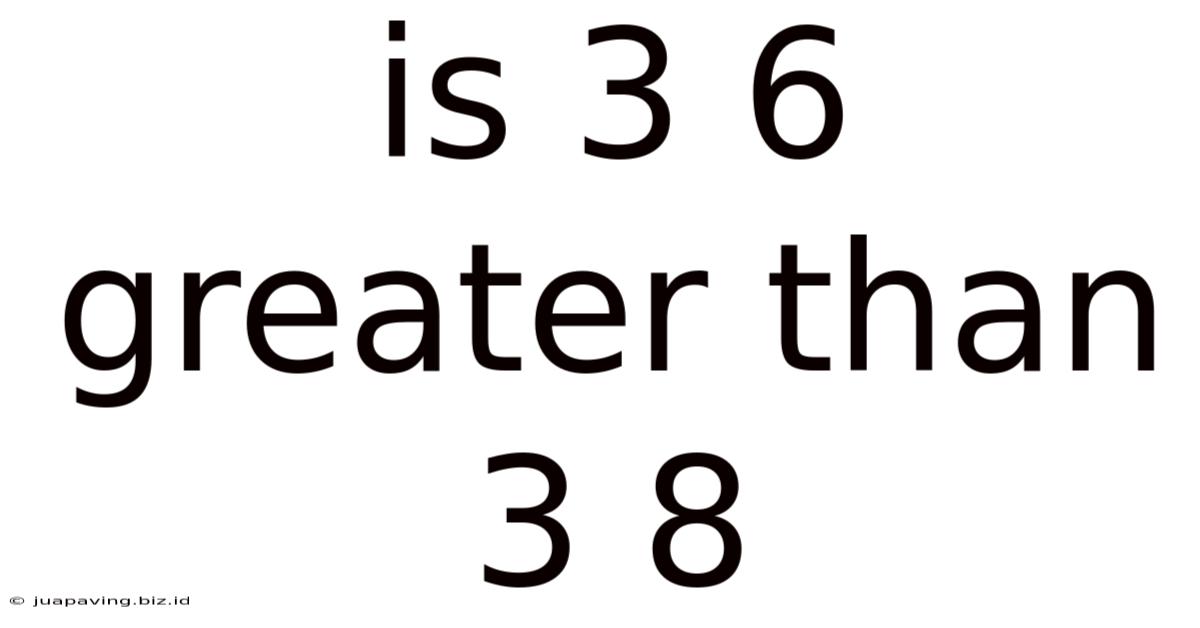
Table of Contents
Is 3/6 Greater Than 3/8? Understanding Fractions and Comparisons
Determining whether 3/6 is greater than 3/8 involves understanding the fundamental principles of fractions and how to compare their values. While the numerators (the top numbers) are the same in both fractions, the denominators (the bottom numbers) differ, significantly impacting their overall value. This article will delve into the intricacies of fraction comparison, providing clear explanations and examples to help you grasp the concept effectively. We'll explore various methods to compare fractions and address common misconceptions. By the end, you'll not only know the answer to the initial question but also possess a solid understanding of how to compare fractions confidently.
Understanding Fractions: A Quick Refresher
Before diving into the comparison, let's ensure we have a firm grasp on the basics of fractions. A fraction represents a part of a whole. It's composed of two key elements:
- Numerator: The top number represents the number of parts we have.
- Denominator: The bottom number represents the total number of equal parts the whole is divided into.
For example, in the fraction 3/6, the numerator (3) indicates we have three parts, and the denominator (6) indicates the whole is divided into six equal parts.
Comparing Fractions: Different Approaches
There are several ways to compare fractions. Let's explore the most common and effective methods:
Method 1: Finding a Common Denominator
This is arguably the most straightforward and widely used method. The core idea is to convert both fractions to equivalent fractions with the same denominator. Once they share a common denominator, comparing the numerators directly determines which fraction is larger.
To find a common denominator for 3/6 and 3/8, we need to find the least common multiple (LCM) of 6 and 8. The LCM is the smallest number that is a multiple of both 6 and 8. In this case, the LCM of 6 and 8 is 24.
Now, we convert both fractions to have a denominator of 24:
-
3/6: To get a denominator of 24, we multiply both the numerator and the denominator by 4 (24/6 = 4). This gives us (3 x 4) / (6 x 4) = 12/24.
-
3/8: To get a denominator of 24, we multiply both the numerator and the denominator by 3 (24/8 = 3). This gives us (3 x 3) / (8 x 3) = 9/24.
Now, comparing 12/24 and 9/24 is simple: 12/24 is greater than 9/24 because 12 > 9.
Therefore, 3/6 is greater than 3/8.
Method 2: Simplifying Fractions Before Comparison
Sometimes, simplifying fractions before comparison can make the process easier. Simplifying means reducing the fraction to its lowest terms by dividing both the numerator and the denominator by their greatest common divisor (GCD).
Let's simplify 3/6: The GCD of 3 and 6 is 3. Dividing both the numerator and the denominator by 3 gives us 1/2.
Now we compare 1/2 and 3/8. We can use the common denominator method again:
The LCM of 2 and 8 is 8.
- 1/2 becomes 4/8 (multiplying both by 4)
Now we compare 4/8 and 3/8. Clearly, 4/8 > 3/8.
Again, we conclude that 3/6 is greater than 3/8.
Method 3: Visual Representation (For Beginners)
For those new to fractions, a visual representation can be incredibly helpful. Imagine two pizzas:
- Pizza 1: Cut into 6 equal slices, with 3 slices taken.
- Pizza 2: Cut into 8 equal slices, with 3 slices taken.
Visually, it's clear that a larger portion of Pizza 1 (3 out of 6) is taken compared to Pizza 2 (3 out of 8). This visual approach reinforces the understanding that 3/6 is greater than 3/8.
Addressing Common Misconceptions
A common mistake is focusing solely on the numerators when comparing fractions. Remember, the denominator plays a crucial role in determining the fraction's value. A larger denominator indicates that the whole is divided into more parts, making each individual part smaller.
Expanding on Fraction Comparison: More Complex Scenarios
The methods discussed above provide a solid foundation for comparing fractions. Let's expand on this by considering more complex scenarios:
-
Comparing Fractions with Different Numerators and Denominators: If you encounter fractions with different numerators and denominators, such as 5/7 and 3/4, you'll still need to find a common denominator (in this case, 28) and then compare the resulting numerators.
-
Comparing Mixed Numbers: Mixed numbers contain a whole number and a fraction (e.g., 2 1/3). To compare mixed numbers, you can convert them into improper fractions (where the numerator is larger than the denominator) and then apply the methods discussed earlier. For example, 2 1/3 would become 7/3.
-
Using Decimals for Comparison: Another approach is to convert fractions into decimals. For instance, 3/6 = 0.5 and 3/8 = 0.375. Comparing decimals is often simpler; 0.5 > 0.375.
Real-World Applications of Fraction Comparison
Understanding fraction comparison isn't just an academic exercise. It's a crucial skill with numerous real-world applications:
-
Cooking and Baking: Following recipes often requires understanding and comparing fractions to ensure accurate measurements.
-
Construction and Engineering: Precise measurements are paramount in these fields, and fraction comparison ensures accuracy in calculations.
-
Finance and Budgeting: Managing finances involves working with percentages and fractions, requiring the ability to compare different values.
-
Data Analysis: Interpreting data often involves working with fractions and percentages, making comparison skills essential for drawing accurate conclusions.
Conclusion: Mastering Fraction Comparison
The ability to compare fractions accurately is a fundamental skill with broad applications. While the initial question – "Is 3/6 greater than 3/8?" – might seem simple, understanding the underlying principles of fractions and the various methods for comparison equips you to tackle more complex scenarios with confidence. By mastering these techniques, you'll enhance your mathematical skills and improve your ability to solve problems across various domains. Remember to practice regularly to solidify your understanding and build your confidence in handling fractions effectively. With consistent effort, comparing fractions will become second nature, allowing you to tackle more complex mathematical challenges with ease and precision.
Latest Posts
Latest Posts
-
Weathering Is The Process Of Breaking Down Rock Into Smaller
May 09, 2025
-
75 As Product Of Prime Factors
May 09, 2025
-
Differentiate Between Diffusion And Active Transport
May 09, 2025
-
What Is The Area Of The Parallelogram In Square Centimeters
May 09, 2025
-
Which Element Has The Greatest Electronegativity
May 09, 2025
Related Post
Thank you for visiting our website which covers about Is 3 6 Greater Than 3 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.