Is 3 4 Greater Than 6 8
Juapaving
May 13, 2025 · 5 min read
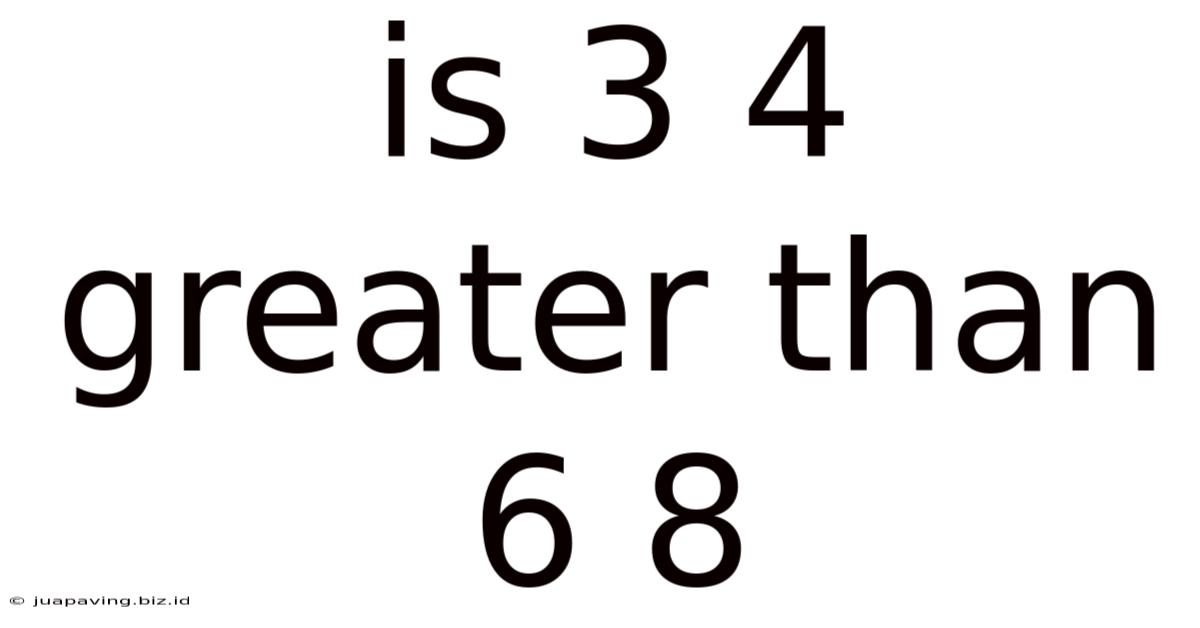
Table of Contents
Is 3/4 Greater Than 6/8? A Deep Dive into Fraction Comparison
The question, "Is 3/4 greater than 6/8?", might seem simple at first glance. For those well-versed in fractions, the answer is readily apparent. However, for others, understanding the underlying principles of fraction comparison is crucial. This article will not only answer this specific question but also provide a comprehensive guide to comparing fractions, equipping you with the tools to tackle similar problems with confidence. We will explore various methods, from visual representations to mathematical calculations, ensuring a thorough understanding of this fundamental mathematical concept.
Understanding Fractions: A Quick Recap
Before diving into the comparison, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates the number of parts we have, while the denominator indicates the total number of equal parts the whole is divided into. For instance, in the fraction 3/4, 3 is the numerator and 4 is the denominator. This means we have 3 parts out of a total of 4 equal parts.
Method 1: Visual Representation
One of the easiest ways to compare fractions is through visual aids. Imagine two identical squares. Divide the first square into four equal parts and shade three of them. This represents the fraction 3/4. Now, divide the second square into eight equal parts and shade six of them. This represents the fraction 6/8. By visually comparing the shaded areas, it becomes clear that both fractions represent the same amount.
Therefore, 3/4 is not greater than 6/8; they are equal.
! (Imagine two squares here, one with 3/4 shaded, the other with 6/8 shaded, visually demonstrating equality)
Method 2: Finding a Common Denominator
A more rigorous mathematical approach involves finding a common denominator for both fractions. A common denominator is a number that is a multiple of both denominators. In this case, the denominators are 4 and 8. Since 8 is a multiple of 4 (4 x 2 = 8), we can use 8 as the common denominator.
To convert 3/4 to an equivalent fraction with a denominator of 8, we multiply both the numerator and denominator by 2:
(3 x 2) / (4 x 2) = 6/8
Now we can easily compare the two fractions: 6/8 and 6/8. Since both fractions are identical, we confirm that:
3/4 = 6/8
Method 3: Simplifying Fractions
Another useful technique is to simplify fractions to their lowest terms. A fraction is in its simplest form when the numerator and denominator have no common factors other than 1. Let's simplify 6/8:
Both 6 and 8 are divisible by 2:
6 ÷ 2 = 3 8 ÷ 2 = 4
Therefore, 6/8 simplifies to 3/4. Again, we see that:
3/4 = 6/8
Method 4: Converting to Decimals
Converting fractions to decimals provides another method for comparison. To convert a fraction to a decimal, divide the numerator by the denominator.
3/4 = 3 ÷ 4 = 0.75 6/8 = 6 ÷ 8 = 0.75
Since both fractions are equal to 0.75, we confirm:
3/4 = 6/8
Beyond the Basic: Comparing Fractions with Different Denominators
The methods outlined above are particularly useful when comparing fractions with different denominators. Let's consider another example: Is 2/3 greater than 5/8?
Using the Common Denominator Method:
The least common multiple (LCM) of 3 and 8 is 24. We convert both fractions to have a denominator of 24:
2/3 = (2 x 8) / (3 x 8) = 16/24 5/8 = (5 x 3) / (8 x 3) = 15/24
Since 16/24 > 15/24, we conclude that:
2/3 > 5/8
Using the Decimal Conversion Method:
2/3 ≈ 0.667 5/8 = 0.625
Again, we see that 0.667 > 0.625, confirming that:
2/3 > 5/8
Advanced Concepts: Improper Fractions and Mixed Numbers
The principles of fraction comparison extend to improper fractions (where the numerator is greater than or equal to the denominator) and mixed numbers (a combination of a whole number and a fraction).
Comparing Improper Fractions: Consider 7/4 and 9/5. We can find a common denominator (20) or convert them to decimals to compare:
7/4 = 1.75 9/5 = 1.8
Therefore, 9/5 > 7/4.
Comparing Mixed Numbers: Consider 2 1/3 and 2 2/5. We can convert them to improper fractions:
2 1/3 = 7/3 2 2/5 = 12/5
Finding a common denominator (15):
7/3 = 35/15 12/5 = 36/15
Therefore, 2 2/5 > 2 1/3.
The Importance of Mastering Fraction Comparison
The ability to compare fractions is a fundamental skill in mathematics, with applications in various fields, including:
- Everyday life: Dividing recipes, measuring ingredients, understanding discounts, etc.
- Science: Analyzing data, calculating ratios, and understanding proportions.
- Engineering: Designing structures, calculating measurements, and solving equations.
- Finance: Calculating interest rates, managing budgets, and analyzing investments.
Conclusion: A Solid Foundation in Fractions
Understanding how to compare fractions is essential for success in mathematics and many other areas. Whether you use visual representations, common denominators, decimal conversions, or simplification, the key is to choose the method that best suits your understanding and the specific problem you're tackling. By mastering these techniques, you can confidently tackle any fraction comparison with ease and accuracy. Remember, the initial question, "Is 3/4 greater than 6/8?", is definitively answered: No, they are equal. This article provides a comprehensive approach to understanding and solving fraction comparisons, ensuring a strong foundation for future mathematical endeavors.
Latest Posts
Latest Posts
-
The Lithosphere Is Divided Into What
May 13, 2025
-
What Is The Chemical Formula Of Magnesium Oxide
May 13, 2025
-
What Is 122 Inches In Feet
May 13, 2025
-
Matter Is Anything That Has And Takes Up
May 13, 2025
-
Parallelogram Abcd With Diagonals Ac And Bd
May 13, 2025
Related Post
Thank you for visiting our website which covers about Is 3 4 Greater Than 6 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.