Is 3 4 Bigger Than 3 5
Juapaving
May 12, 2025 · 5 min read
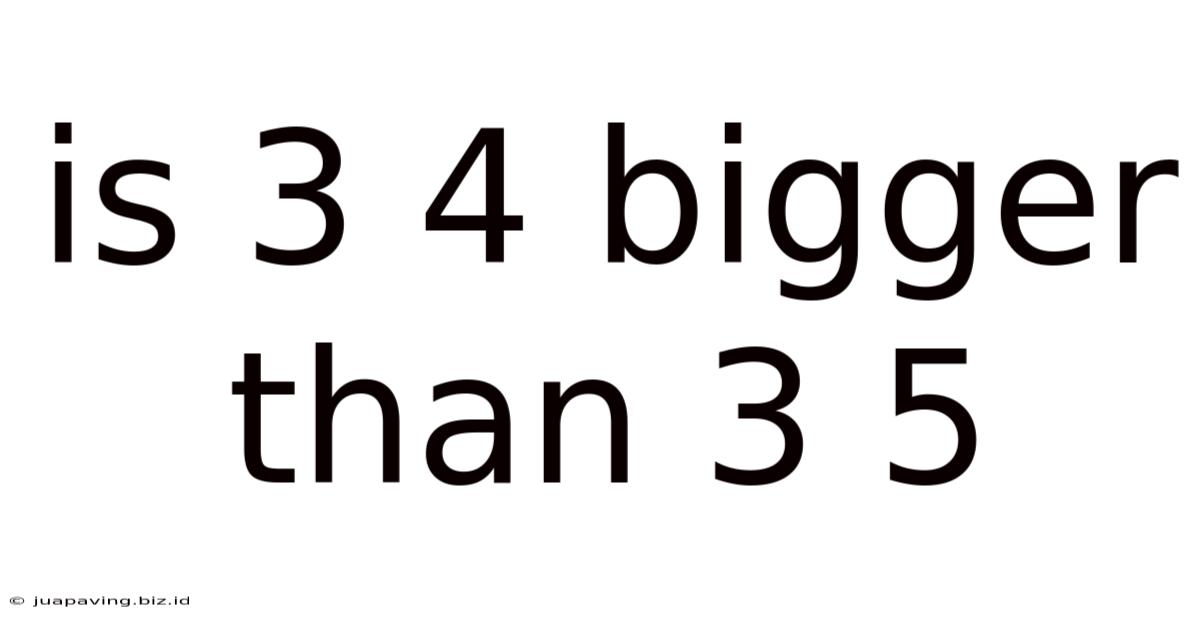
Table of Contents
Is 3/4 Bigger Than 3/5? A Deep Dive into Fraction Comparison
The question, "Is 3/4 bigger than 3/5?" might seem deceptively simple, especially for those comfortable with basic arithmetic. However, understanding the underlying principles behind fraction comparison is crucial for a strong foundation in mathematics and problem-solving. This article will not only answer this specific question but will also explore various methods for comparing fractions, equipping you with the tools to tackle similar problems with confidence.
Understanding Fractions: A Quick Refresher
Before diving into the comparison, let's revisit the fundamental concept of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates the total number of equal parts the whole is divided into, while the numerator shows how many of those parts are being considered.
For instance, in the fraction 3/4, the denominator (4) signifies that the whole is divided into four equal parts, and the numerator (3) indicates that we're considering three of those parts.
Comparing Fractions: Different Approaches
Several methods can be used to compare fractions. Let's explore the most common and effective ones:
1. Visual Comparison
This method is particularly helpful for visualizing the relative sizes of fractions. Imagine two identical pizzas. One is cut into four equal slices (representing 3/4), and the other into five equal slices (representing 3/5). Visually, it's clear that each slice of the pizza cut into four pieces is larger than each slice of the pizza cut into five pieces. Therefore, three slices out of four will be larger than three slices out of five.
This approach works well for smaller fractions, but it becomes less practical with larger or more complex fractions.
2. Finding a Common Denominator
This is a widely used and reliable method for comparing fractions. The core idea is to rewrite both fractions so that they have the same denominator. This allows for a direct comparison of the numerators.
To find a common denominator for 3/4 and 3/5, we need to find the least common multiple (LCM) of 4 and 5. The LCM of 4 and 5 is 20.
Now, we rewrite each fraction with a denominator of 20:
- 3/4: To get a denominator of 20, we multiply both the numerator and the denominator by 5: (3 x 5) / (4 x 5) = 15/20
- 3/5: To get a denominator of 20, we multiply both the numerator and the denominator by 4: (3 x 4) / (5 x 4) = 12/20
Now, comparing 15/20 and 12/20, it's evident that 15/20 (or 3/4) is greater than 12/20 (or 3/5).
3. Converting to Decimals
Another effective method is to convert both fractions into decimals. This involves dividing the numerator by the denominator for each fraction.
- 3/4 = 0.75
- 3/5 = 0.6
By comparing the decimal values, we see that 0.75 is greater than 0.6, confirming that 3/4 is bigger than 3/5.
This method is particularly useful when dealing with fractions that are difficult to compare using common denominators.
4. Cross-Multiplication
This method provides a quick way to compare two fractions without finding a common denominator. It involves multiplying the numerator of the first fraction by the denominator of the second fraction and vice-versa. Then, compare the resulting products.
Let's compare 3/4 and 3/5 using cross-multiplication:
- Multiply the numerator of the first fraction (3) by the denominator of the second fraction (5): 3 x 5 = 15
- Multiply the numerator of the second fraction (3) by the denominator of the first fraction (4): 3 x 4 = 12
Since 15 > 12, we conclude that 3/4 > 3/5.
This method is efficient, especially when dealing with larger fractions. However, it's crucial to remember that the inequality sign follows the direction of the greater product.
The Answer: Yes, 3/4 is Bigger Than 3/5
Using any of the methods described above—visual comparison, common denominators, decimal conversion, or cross-multiplication—we definitively conclude that 3/4 is bigger than 3/5.
Beyond the Basics: Applying Fraction Comparison in Real-World Scenarios
Understanding fraction comparison is not just an academic exercise; it has numerous practical applications in everyday life. Consider these examples:
-
Cooking and Baking: Recipes often involve fractions, and accurate comparisons are crucial for achieving desired results. Knowing if 1/2 cup is more or less than 2/3 cup can make the difference between a delicious cake and a culinary disaster.
-
Construction and Engineering: Precision is paramount in these fields. Accurate fraction comparison is essential for precise measurements and calculations, ensuring structural integrity and safety.
-
Finance and Budgeting: Understanding fractions helps in managing finances effectively. Comparing fractions of budgets or percentages helps in making informed financial decisions.
-
Data Analysis: Data often involves fractions and percentages. The ability to compare fractions is essential for interpreting data accurately and drawing meaningful conclusions.
Mastering Fractions: Tips and Resources
Consistent practice is key to mastering fraction comparison. Here are some tips:
-
Start with the basics: Ensure a strong understanding of fraction concepts before tackling complex comparisons.
-
Use multiple methods: Practice using different methods to compare fractions, as each approach offers unique insights and benefits.
-
Solve practice problems: Numerous online resources and textbooks offer practice problems to reinforce your understanding.
-
Seek help when needed: Don't hesitate to ask for help from teachers, tutors, or online communities if you encounter difficulties.
By understanding and applying these methods, you can confidently tackle any fraction comparison problem, paving the way for greater success in math and beyond. Remember, the key is to understand the underlying principles and choose the method that best suits the specific problem at hand. This deep understanding of fractions will serve as a solid foundation for more advanced mathematical concepts.
Latest Posts
Latest Posts
-
When Acid Reacts With Base What Compounds Are Formed
May 13, 2025
-
Difference Between An Act And Law
May 13, 2025
-
The Anaerobic Breakdown Of Glucose Is Called
May 13, 2025
-
Kinetic Energy Depends On What Two Things
May 13, 2025
-
Home Link 7 9 Perimeter Patterns Answers
May 13, 2025
Related Post
Thank you for visiting our website which covers about Is 3 4 Bigger Than 3 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.