Is 21 A Composite Or Prime Number
Juapaving
May 10, 2025 · 5 min read
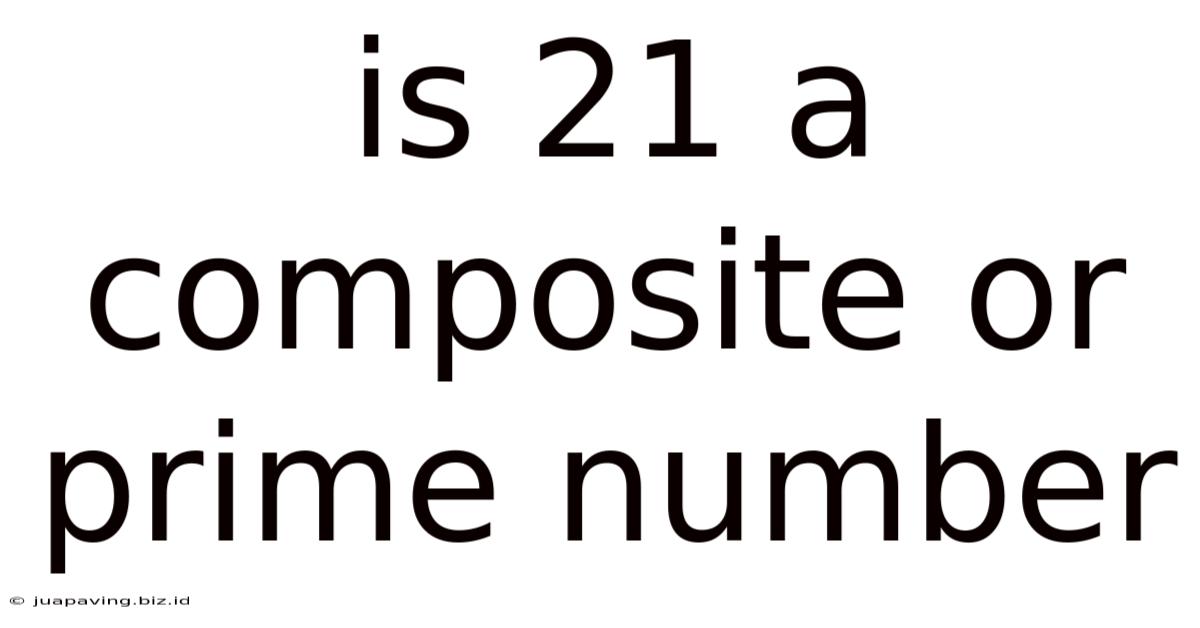
Table of Contents
Is 21 a Composite or Prime Number? A Deep Dive into Number Theory
The question of whether 21 is a composite or prime number might seem trivial at first glance. However, exploring this seemingly simple query opens a fascinating window into the fundamental concepts of number theory, a branch of mathematics dealing with the properties of integers. This article will not only answer the question definitively but also delve into the underlying principles that define prime and composite numbers, explore related mathematical concepts, and illustrate the significance of prime numbers in various fields.
Understanding Prime and Composite Numbers
Before we determine the classification of 21, let's establish a clear understanding of the definitions:
Prime Number: A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. In simpler terms, it's only divisible by 1 and itself without leaving a remainder. Examples include 2, 3, 5, 7, 11, and so on. The number 1 is neither prime nor composite.
Composite Number: A composite number is a natural number greater than 1 that is not prime. This means it has at least one positive divisor other than 1 and itself. Composite numbers can be expressed as a product of prime numbers. For instance, 4 (2 x 2), 6 (2 x 3), 9 (3 x 3), and 12 (2 x 2 x 3) are all composite numbers.
Determining the Nature of 21
Now, let's apply these definitions to the number 21. Is 21 only divisible by 1 and itself? The answer is no. 21 is divisible by 3 (21 / 3 = 7) and 7 (21 / 7 = 3). Since 21 has divisors other than 1 and 21, it does not satisfy the definition of a prime number. Therefore, 21 is a composite number.
Prime Factorization of 21
A crucial concept related to composite numbers is prime factorization. This involves expressing a composite number as a product of its prime factors. For 21, the prime factorization is 3 x 7. This means that 21 can be uniquely represented as the product of the prime numbers 3 and 7. This uniqueness is a cornerstone of number theory and is vital in various mathematical applications.
The Significance of Prime Numbers
Prime numbers might seem like abstract mathematical entities, but their importance extends far beyond theoretical discussions. Their unique properties have profound implications in various fields, including:
Cryptography
Prime numbers are the bedrock of modern cryptography, particularly in public-key cryptography systems like RSA. The security of these systems relies on the difficulty of factoring very large composite numbers into their prime factors. The computational effort required for factoring large numbers with many digits makes it practically impossible to break the encryption in a reasonable timeframe.
Computer Science
Prime numbers play a vital role in various algorithms and data structures used in computer science. Hash tables, for example, often utilize prime numbers to minimize collisions and improve efficiency. Also, certain aspects of network routing and error correction codes depend on properties of prime numbers.
Number Theory and Abstract Algebra
Prime numbers are fundamental objects of study in number theory and abstract algebra. Many theorems and conjectures in these fields revolve around the properties and distribution of prime numbers. Understanding prime numbers is essential to grasp various concepts in these areas, including modular arithmetic, algebraic number theory, and group theory.
Exploring Related Concepts
Several related concepts further enrich our understanding of prime and composite numbers:
Sieve of Eratosthenes
The Sieve of Eratosthenes is an ancient algorithm for finding all prime numbers up to any given limit. It's an elegant and efficient method that systematically eliminates composite numbers, leaving only prime numbers. Understanding this algorithm helps visualize the distribution of prime numbers within a given range.
Twin Primes
Twin primes are pairs of prime numbers that differ by 2 (e.g., 3 and 5, 5 and 7, 11 and 13). The study of twin primes is an active area of research in number theory, with the twin prime conjecture postulating that there are infinitely many twin prime pairs.
Mersenne Primes
Mersenne primes are prime numbers that are one less than a power of 2 (e.g., 3, 7, 31, 127). Finding Mersenne primes is a computationally intensive task, and the Great Internet Mersenne Prime Search (GIMPS) project actively seeks these large prime numbers.
Goldbach's Conjecture
Goldbach's Conjecture is one of the oldest and most famous unsolved problems in number theory. It states that every even integer greater than 2 can be expressed as the sum of two prime numbers. Despite extensive testing, this conjecture remains unproven.
Conclusion: The Importance of Understanding Prime and Composite Numbers
Determining whether 21 is a composite or prime number serves as a springboard for exploring a vast and intricate world within mathematics. The seemingly simple distinction between prime and composite numbers has profound implications in various fields, highlighting the importance of understanding their properties and applications. From securing online transactions to advancing theoretical mathematics, the significance of prime numbers continues to shape our understanding of the world around us. The core takeaway is that while 21 is definitively a composite number (3 x 7), its very nature provides a lens through which to appreciate the richness and depth of number theory and its widespread impact. Further exploration of these concepts will undoubtedly reveal even more fascinating aspects of this essential mathematical field.
Latest Posts
Latest Posts
-
How Many Feet Are In 118 In
May 10, 2025
-
Arrange The Following Events In China In Chronological Order
May 10, 2025
-
Which Is The Largest Sense Organ
May 10, 2025
-
Which Of The Following Is An Example Of Convection
May 10, 2025
-
How Many Chromosomes In The Human Egg Cell
May 10, 2025
Related Post
Thank you for visiting our website which covers about Is 21 A Composite Or Prime Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.