Is 2 5 Greater Than 3 8
Juapaving
May 12, 2025 · 5 min read
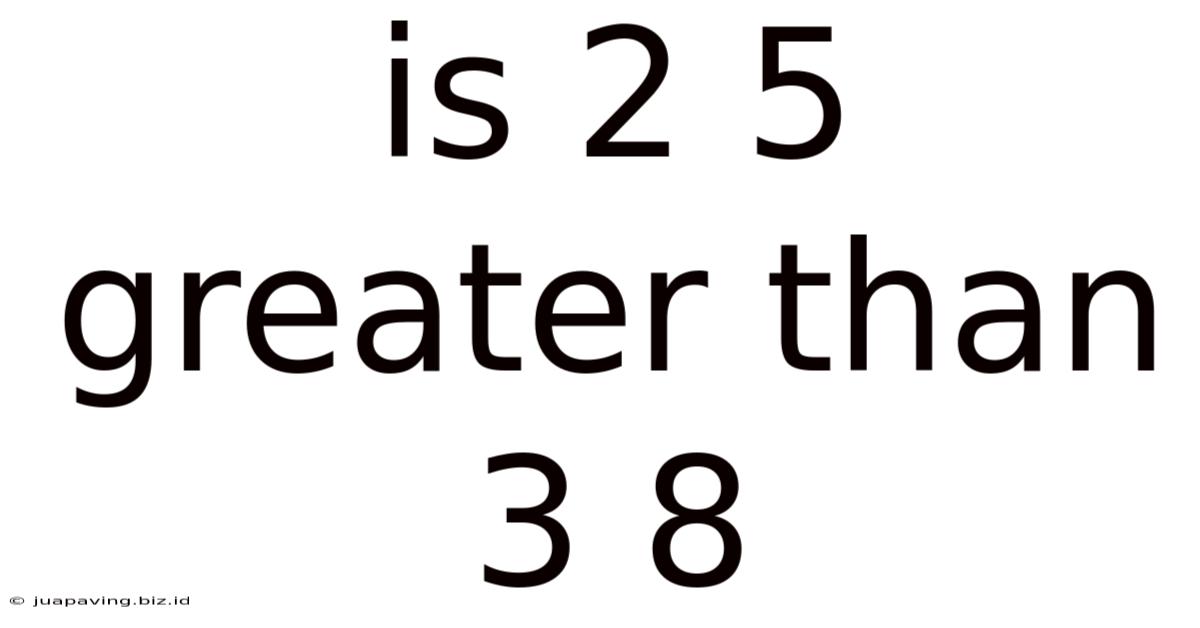
Table of Contents
Is 2/5 Greater Than 3/8? A Comprehensive Comparison
Determining whether 2/5 is greater than 3/8 might seem like a simple task, particularly for those comfortable with fractions. However, understanding the underlying principles and exploring various comparison methods provides a valuable opportunity to solidify foundational math skills. This article will delve into several approaches to solve this problem, explaining the logic behind each method and offering insights into fraction comparison strategies.
Understanding Fractions: A Quick Recap
Before diving into the comparison, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into.
For instance, in the fraction 2/5, the numerator is 2, and the denominator is 5. This means we have 2 out of 5 equal parts of a whole.
Method 1: Finding a Common Denominator
This is a classic and reliable method for comparing fractions. The core idea is to rewrite both fractions so they share the same denominator. This allows for a direct comparison of the numerators.
Steps:
-
Find the least common multiple (LCM) of the denominators: The denominators are 5 and 8. The LCM of 5 and 8 is 40 (5 x 8 = 40).
-
Convert the fractions:
- To convert 2/5 to a fraction with a denominator of 40, we multiply both the numerator and denominator by 8: (2 x 8) / (5 x 8) = 16/40
- To convert 3/8 to a fraction with a denominator of 40, we multiply both the numerator and denominator by 5: (3 x 5) / (8 x 5) = 15/40
-
Compare the numerators: Now we compare 16/40 and 15/40. Since 16 > 15, we conclude that 16/40 > 15/40, and therefore, 2/5 > 3/8.
Method 2: Converting to Decimals
Another effective way to compare fractions is to convert them into decimals. This method is particularly helpful when dealing with more complex fractions or when a quick numerical comparison is needed.
Steps:
-
Divide the numerator by the denominator for each fraction:
- 2/5 = 2 ÷ 5 = 0.4
- 3/8 = 3 ÷ 8 = 0.375
-
Compare the decimal values: Since 0.4 > 0.375, we conclude that 2/5 > 3/8.
Method 3: Visual Representation (Using a Diagram)
Visual aids can be incredibly beneficial for understanding fraction comparisons, especially for those who are visual learners. We can represent each fraction using a diagram.
Steps:
-
Draw two rectangles of equal size. Each rectangle will represent a whole.
-
Divide the first rectangle into 5 equal parts and shade 2 of them to represent 2/5.
-
Divide the second rectangle into 8 equal parts and shade 3 of them to represent 3/8.
-
Compare the shaded areas. Visually, it will be apparent that the shaded area in the first rectangle (representing 2/5) is larger than the shaded area in the second rectangle (representing 3/8). This confirms that 2/5 > 3/8.
Method 4: Cross-Multiplication
This method is a shortcut for comparing two fractions and is based on the principle of equivalent fractions.
Steps:
-
Cross-multiply the numerators and denominators:
- Multiply the numerator of the first fraction (2) by the denominator of the second fraction (8): 2 x 8 = 16
- Multiply the numerator of the second fraction (3) by the denominator of the first fraction (5): 3 x 5 = 15
-
Compare the products: Since 16 > 15, we conclude that 2/5 > 3/8.
This method essentially compares the relative sizes of the fractions without explicitly finding a common denominator. If the product of the numerator of the first fraction and the denominator of the second fraction is larger, then the first fraction is larger.
Understanding the Magnitude of the Difference
While we've established that 2/5 is greater than 3/8, it's also insightful to understand the magnitude of the difference. Using decimal representation, we found that 2/5 is 0.4 and 3/8 is 0.375. The difference is 0.4 - 0.375 = 0.025. This relatively small difference highlights that the two fractions are quite close in value.
Practical Applications and Real-World Examples
The ability to compare fractions isn't just an abstract mathematical skill; it has numerous practical applications in everyday life. Consider these examples:
-
Cooking: Following a recipe often involves working with fractions of ingredients. Knowing which fraction is larger helps ensure accurate measurements.
-
Construction: Accurate measurements are crucial in construction projects. Comparing fractions is essential when working with blueprints and dimensions.
-
Finance: Understanding fractions is fundamental to managing personal finances. Calculating percentages, interest rates, and proportions often involves fraction comparison.
Beyond the Basics: Extending Fraction Comparison Skills
While the methods described above effectively compare 2/5 and 3/8, they provide a foundation for tackling more complex fraction comparisons. Mastering these techniques prepares you to handle larger numbers, mixed numbers (whole numbers and fractions), and more intricate fraction operations.
Conclusion: 2/5 is Indeed Greater Than 3/8
Through various methods – finding a common denominator, converting to decimals, visual representation, and cross-multiplication – we've conclusively demonstrated that 2/5 is greater than 3/8. Understanding these different approaches not only solves this specific problem but also equips you with the tools and knowledge to confidently compare any pair of fractions. The key is to choose the method that best suits your understanding and the complexity of the fractions involved. Remember to practice regularly to solidify these important mathematical skills. The more comfortable you become with fractions, the easier it will be to navigate various real-world applications where fractional comparisons are necessary.
Latest Posts
Latest Posts
-
The Substance That Is Dissolved In The Solution
May 13, 2025
-
Newtons First Law Of Motion Examples In Everyday Life
May 13, 2025
-
How To Find Number Of Molecules
May 13, 2025
-
Different Kinds Of Lines In Math
May 13, 2025
-
Which Of The Following Is A Protein
May 13, 2025
Related Post
Thank you for visiting our website which covers about Is 2 5 Greater Than 3 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.