Is 2 3 Greater Than 2 5
Juapaving
May 09, 2025 · 5 min read
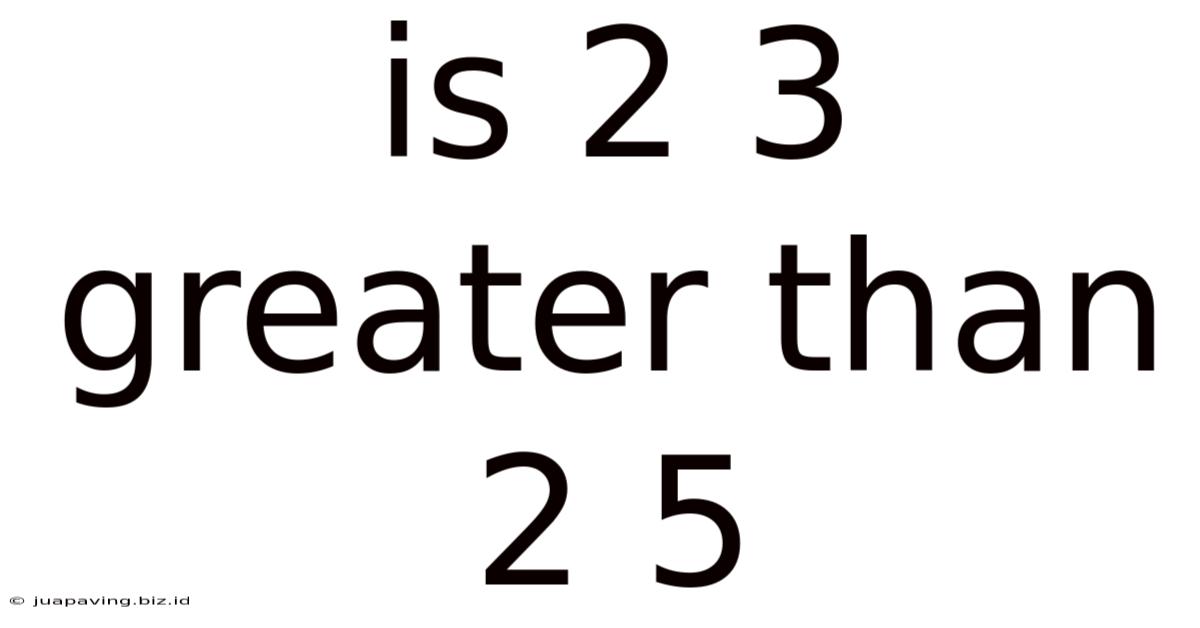
Table of Contents
Is 2/3 Greater Than 2/5? A Deep Dive into Fraction Comparison
The seemingly simple question, "Is 2/3 greater than 2/5?", opens a door to a deeper understanding of fractions, a fundamental concept in mathematics. While the answer itself is straightforward, exploring the various methods to arrive at the solution and the underlying principles strengthens mathematical intuition and problem-solving skills. This article will not only answer the question definitively but also explore several approaches to comparing fractions, ensuring a comprehensive understanding for readers of all levels.
Understanding Fractions: The Building Blocks
Before diving into the comparison, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates the number of parts we have, while the denominator indicates the total number of equal parts the whole is divided into.
In our case, we have two fractions: 2/3 and 2/5. In 2/3, the numerator (2) represents two parts, and the denominator (3) signifies that the whole is divided into three equal parts. Similarly, in 2/5, we have two parts out of a whole divided into five equal parts.
Method 1: Visual Representation
A visual approach can be incredibly helpful, especially for beginners. Imagine two identical circles.
Visualizing 2/3:
Divide the first circle into three equal sections. Shade two of these sections. This visually represents 2/3.
Visualizing 2/5:
Divide the second circle into five equal sections. Shade two of these sections. This visually represents 2/5.
By comparing the shaded areas, it becomes immediately apparent that the shaded area representing 2/3 is larger than the shaded area representing 2/5. This visual comparison provides a clear and intuitive understanding of which fraction is greater.
Method 2: Finding a Common Denominator
This is a more formal mathematical approach. To compare fractions effectively, it's often necessary to find a common denominator, which is a common multiple of the denominators of the fractions. This allows for a direct comparison of the numerators.
The denominators in our example are 3 and 5. The least common multiple (LCM) of 3 and 5 is 15.
Converting to a Common Denominator:
- 2/3: To convert the denominator to 15, we multiply both the numerator and the denominator by 5: (2 x 5) / (3 x 5) = 10/15
- 2/5: To convert the denominator to 15, we multiply both the numerator and the denominator by 3: (2 x 3) / (5 x 3) = 6/15
Now that both fractions have the same denominator (15), we can directly compare the numerators. Since 10 > 6, we can conclude that 10/15 (or 2/3) is greater than 6/15 (or 2/5).
Method 3: Decimal Conversion
Converting fractions to decimals provides another method for comparison.
Converting to Decimals:
- 2/3: 2 ÷ 3 ≈ 0.6667
- 2/5: 2 ÷ 5 = 0.4
Comparing the decimal values, 0.6667 > 0.4, confirming that 2/3 is greater than 2/5. This method is particularly useful when dealing with fractions that are difficult to visualize or convert to a common denominator easily.
Method 4: Cross-Multiplication
Cross-multiplication offers a quick and efficient way to compare two fractions. This method involves multiplying the numerator of one fraction by the denominator of the other and vice versa.
Cross-Multiplication:
- Multiply the numerator of 2/3 (2) by the denominator of 2/5 (5): 2 x 5 = 10
- Multiply the numerator of 2/5 (2) by the denominator of 2/3 (3): 2 x 3 = 6
Compare the results: 10 > 6. Since the result of multiplying the numerator of 2/3 by the denominator of 2/5 is greater, we conclude that 2/3 is greater than 2/5.
Understanding the Underlying Principle: The Relationship Between Numerators and Denominators
The key to understanding fraction comparison lies in grasping the inverse relationship between the numerator and the denominator. For a given numerator, a smaller denominator indicates a larger fraction because the whole is divided into fewer parts, making each part larger.
In our example, both fractions have the same numerator (2). Since the denominator of 2/3 (3) is smaller than the denominator of 2/5 (5), 2/3 represents a larger portion of the whole than 2/5.
Beyond the Basics: Extending the Concept
The methods discussed above are applicable to comparing any two fractions. However, more complex scenarios might require additional techniques, such as simplifying fractions before comparison or working with mixed numbers (numbers containing both a whole number and a fraction).
Simplifying Fractions:
Before comparing, simplifying fractions to their lowest terms can make the comparison easier. For example, if comparing 6/12 and 2/5, simplifying 6/12 to 1/2 would make the comparison more straightforward.
Comparing Mixed Numbers:
When comparing mixed numbers, convert them to improper fractions (where the numerator is larger than the denominator) before applying any of the previously discussed methods.
Conclusion: Mastering Fraction Comparison
The question "Is 2/3 greater than 2/5?" provides a launching pad for exploring the fascinating world of fractions. By mastering various comparison methods—visual representation, finding a common denominator, decimal conversion, and cross-multiplication—we build a strong foundation in mathematical reasoning and problem-solving. Remember to always understand the underlying principles of numerators and denominators to enhance your understanding and confidence when dealing with fractions. The seemingly simple task of comparing fractions becomes a valuable exercise in building a robust understanding of mathematical concepts. This knowledge extends far beyond simple arithmetic, proving essential in higher-level mathematics and numerous real-world applications.
Latest Posts
Latest Posts
-
Difference Between Nadh And Nadph In Humans
May 10, 2025
-
The Quotient Of A Number And 4 Is
May 10, 2025
-
What Is An Example Of Longitudinal Wave
May 10, 2025
-
What Part Of The Cell Maintains Homeostasis
May 10, 2025
-
Can Displacement Be Greater Than Distance
May 10, 2025
Related Post
Thank you for visiting our website which covers about Is 2 3 Greater Than 2 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.