Is 2 3 Greater Than 2 4
Juapaving
May 11, 2025 · 4 min read
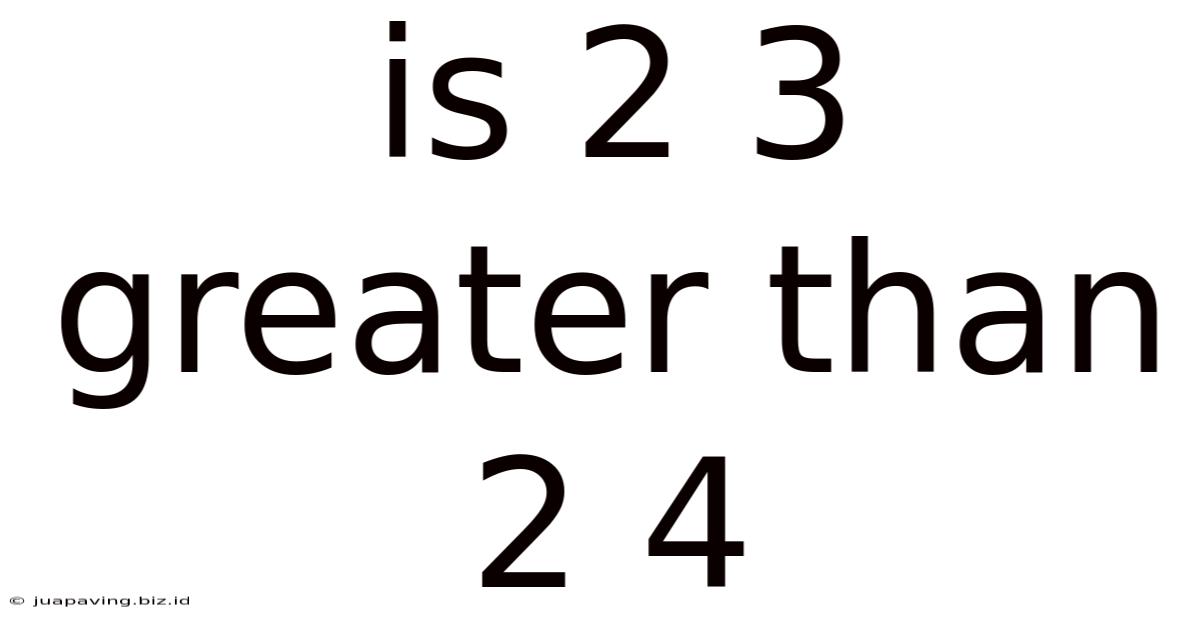
Table of Contents
Is 2³ Greater Than 2⁴? Understanding Exponential Growth
The question, "Is 2³ greater than 2⁴?", seems deceptively simple. At first glance, it might appear that a larger exponent automatically means a larger number. However, understanding the principles behind exponential growth reveals a more nuanced answer. This article will delve into the concept of exponents, explore why 2⁴ is greater than 2³, and discuss the broader implications of exponential growth in various fields.
Understanding Exponents
Before we tackle the core question, let's solidify our understanding of exponents. An exponent, also known as a power or index, indicates how many times a number (the base) is multiplied by itself. In the expressions 2³ and 2⁴, the base is 2. The exponent signifies the number of times 2 is multiplied.
-
2³ (Two cubed or Two to the power of three): This means 2 multiplied by itself three times: 2 * 2 * 2 = 8.
-
2⁴ (Two to the power of four): This means 2 multiplied by itself four times: 2 * 2 * 2 * 2 = 16.
Comparing 2³ and 2⁴
Now, let's directly compare the results:
- 2³ = 8
- 2⁴ = 16
Clearly, 16 is greater than 8. Therefore, 2⁴ is greater than 2³.
The Significance of Exponential Growth
The seemingly simple comparison above highlights a crucial concept: exponential growth. Exponential growth isn't simply about adding a constant value; it's about multiplying by a constant value repeatedly. This leads to a rapid increase in the value as the exponent increases.
Imagine you have a single bacterium that doubles every hour. After one hour, you have 2 bacteria (2¹). After two hours, you have 4 bacteria (2²). After three hours, you have 8 bacteria (2³), and after four hours, you have 16 bacteria (2⁴). Notice how the number of bacteria increases dramatically over time – this is the power of exponential growth.
Exponential Growth in Real-World Scenarios
Exponential growth is not confined to theoretical mathematics; it manifests itself in various real-world scenarios:
-
Population Growth: Under ideal conditions, populations (human, animal, or bacterial) can exhibit exponential growth, increasing at an accelerating rate.
-
Compound Interest: The interest earned on savings accounts or investments is often compounded, meaning the interest earned also earns interest, leading to exponential growth of the principal amount.
-
Viral Spread: The spread of infectious diseases or viral content online can follow an exponential pattern, with each infected individual infecting multiple others.
-
Technological Advancements: Moore's Law, which predicts the doubling of transistors on a microchip approximately every two years, exemplifies exponential growth in the technology sector.
Beyond 2³ and 2⁴: Exploring Larger Exponents
Let's extend our understanding by comparing numbers with larger exponents:
- 2⁵ = 32
- 2⁶ = 64
- 2⁷ = 128
- 2⁸ = 256
- 2⁹ = 512
- 2¹⁰ = 1024
As you can see, the values increase exponentially. The difference between consecutive powers of 2 also increases rapidly. This showcases the accelerating nature of exponential growth.
Understanding the Relationship Between Base and Exponent
The base in an exponential expression significantly influences the rate of growth. Let's compare 2⁴ with other bases:
- 3⁴ = 81
- 4⁴ = 256
- 5⁴ = 625
Even with the same exponent (4), changing the base dramatically alters the final value. A larger base leads to significantly faster exponential growth.
Exponential Decay: The Counterpart of Exponential Growth
While we've focused on exponential growth, it's essential to acknowledge exponential decay. This occurs when a quantity decreases by a constant factor over time. For example, the decay of radioactive isotopes follows an exponential decay pattern.
The formula for exponential decay often involves a fraction as the base (e.g., 0.5 raised to the power of time). This means the quantity decreases by half with each unit of time.
Practical Applications and Implications
Understanding exponential growth and decay has numerous practical applications across various disciplines:
-
Finance: Predicting future investment values, understanding loan repayments, and modeling economic growth.
-
Biology: Modeling population dynamics, analyzing the spread of diseases, and understanding cellular processes.
-
Physics: Analyzing radioactive decay, understanding the growth and decay of physical phenomena.
-
Computer Science: Analyzing algorithms' efficiency, understanding data growth in databases, and modeling network traffic.
Conclusion: The Importance of Understanding Exponents
The seemingly simple comparison of 2³ and 2⁴ reveals the profound implications of exponential growth. By understanding the principles behind exponents, we gain insight into a wide range of phenomena, from the growth of populations to the spread of information. This knowledge is crucial for making informed decisions in various fields and for appreciating the powerful influence of exponential growth and decay in our world. Remember, a larger exponent doesn't always mean a larger number – the base plays a crucial role. But with a consistent base, a higher exponent will always result in a larger outcome, as illustrated by the clear superiority of 2⁴ over 2³.
Latest Posts
Latest Posts
-
Select The Star Life Cycle That Is Accurate
May 11, 2025
-
Which Of The Following Is Not A Mineral
May 11, 2025
-
In Which Stage Of Meiosis Crossing Over Takes Place
May 11, 2025
-
How Many Chromosomes Are Present In A Human Gamete
May 11, 2025
-
Which Expression Is Equivalent To The Expression Shown
May 11, 2025
Related Post
Thank you for visiting our website which covers about Is 2 3 Greater Than 2 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.