Is 1 8 Greater Than 1 2
Juapaving
May 11, 2025 · 5 min read
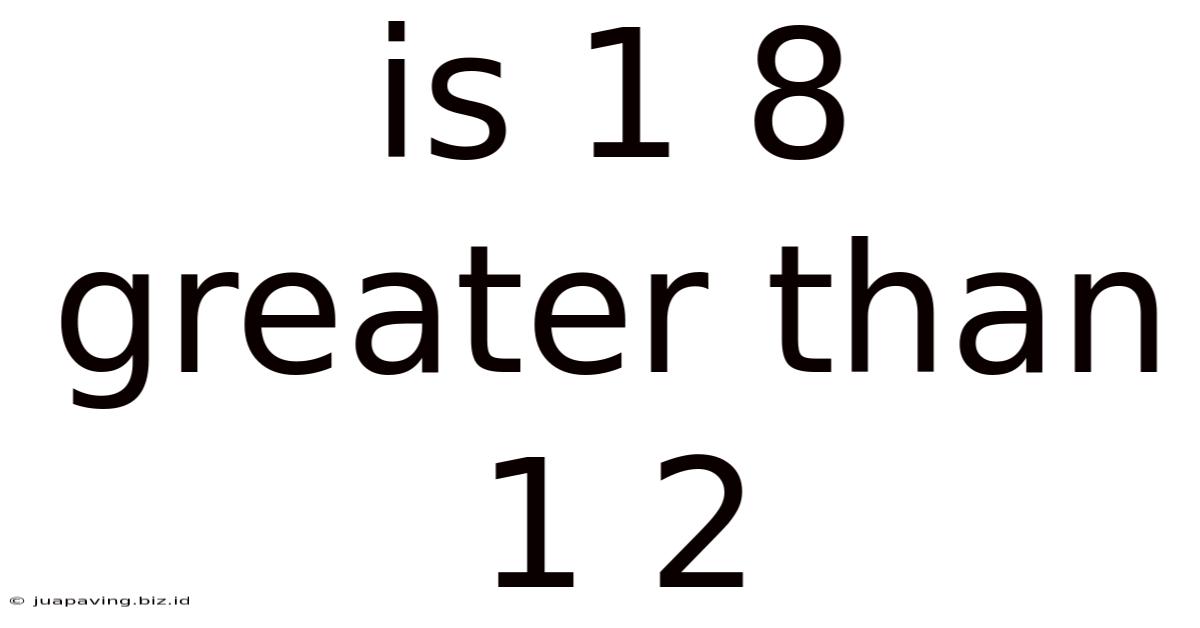
Table of Contents
Is 1/8 Greater Than 1/2? Understanding Fraction Comparison
The question, "Is 1/8 greater than 1/2?" might seem simple at first glance, but it touches upon a fundamental concept in mathematics: understanding and comparing fractions. This article will delve into the intricacies of fraction comparison, providing a clear and comprehensive explanation of why 1/8 is not greater than 1/2, and exploring various methods to compare fractions effectively. We'll also look at practical applications and common misconceptions to solidify your understanding.
Visualizing Fractions: A Picture is Worth a Thousand Words
One of the easiest ways to grasp the relative sizes of fractions is through visualization. Imagine a pizza cut into eight equal slices (representing 1/8). Now imagine another pizza cut into only two equal slices (representing 1/2). Which slice is larger? Clearly, one half (1/2) of the pizza is significantly larger than one-eighth (1/8) of the pizza.
This visual representation helps illustrate the core concept: the smaller the denominator (the bottom number in a fraction), the larger the portion represented. In our example, the denominator of 1/2 (which is 2) is smaller than the denominator of 1/8 (which is 8), therefore 1/2 represents a larger portion.
Understanding Fraction Basics: Numerator and Denominator
Before delving deeper, let's refresh our understanding of the components of a fraction:
- Numerator: The top number of a fraction, representing the number of parts you have.
- Denominator: The bottom number of a fraction, representing the total number of equal parts the whole is divided into.
In the fractions 1/8 and 1/2, both have a numerator of 1, indicating we have one part. The difference lies in the denominators: 8 and 2. The denominator dictates the size of each part.
Comparing Fractions: Methods and Techniques
There are several effective methods to compare fractions:
1. Using Visual Aids: (Already Explained Above)
Visual aids are especially useful for beginners and for reinforcing the conceptual understanding of fraction sizes. Drawings, diagrams, or even physical objects can be used to represent fractions and compare their relative sizes.
2. Finding a Common Denominator: The Gold Standard
This is a robust and reliable method for comparing any two fractions. The process involves finding a common multiple of the two denominators. This common multiple becomes the new denominator for both fractions. We then adjust the numerators accordingly to maintain the fraction's value.
Let's compare 1/8 and 1/2 using this method:
- Find a common denominator: The least common multiple of 8 and 2 is 8.
- Convert the fractions:
- 1/2 remains as 1/2 because it already has a denominator of 8.
- To convert 1/2 to have a denominator of 8, we multiply both the numerator and denominator by 4: (1 * 4) / (2 * 4) = 4/8
- Compare: Now we compare 1/8 and 4/8. Clearly, 4/8 (or 1/2) is greater than 1/8.
3. Converting to Decimals: A Numerical Approach
Converting fractions to decimals provides another way to compare them. This method is particularly useful when dealing with more complex fractions or when you prefer a numerical comparison.
To convert a fraction to a decimal, divide the numerator by the denominator:
- 1/8 = 0.125
- 1/2 = 0.5
Comparing 0.125 and 0.5, it's evident that 0.5 (or 1/2) is larger than 0.125 (or 1/8).
4. Using Number Lines: A Visual Comparison Tool
A number line provides a visual representation of the relative positions of fractions. Mark 0 and 1 on the number line, and then divide the space between them into equal parts based on the denominators of the fractions. Plotting the fractions on the number line allows for easy visual comparison.
Common Misconceptions about Fraction Comparison
Several misconceptions can hinder the understanding of fraction comparison. Let's address some of them:
- Focusing solely on the numerator: It's crucial to remember that comparing numerators alone is insufficient. The denominator plays an equally important role in determining the size of the fraction.
- Assuming larger numbers mean larger fractions: A larger numerator does not always indicate a larger fraction. The denominator's influence must be considered.
- Ignoring equivalent fractions: Two fractions can represent the same value even if their numerators and denominators are different (e.g., 1/2 and 2/4). Recognizing and working with equivalent fractions is crucial for accurate comparison.
Practical Applications of Fraction Comparison
Understanding fraction comparison is fundamental to various aspects of life:
- Cooking and Baking: Following recipes often requires understanding fractional amounts of ingredients.
- Construction and Engineering: Precise measurements and calculations in construction rely on accurate fraction comparison.
- Finance and Budgeting: Managing money often involves working with fractions of amounts.
- Data Analysis: Interpreting data often involves understanding proportions and percentages, which are based on fractions.
Conclusion: 1/8 is Definitely Smaller Than 1/2
Through visual representation, common denominator method, decimal conversion, and number line comparison, we have conclusively shown that 1/8 is not greater than 1/2. In fact, 1/2 is significantly larger than 1/8. Mastering the techniques outlined in this article will equip you to confidently compare fractions and apply this crucial mathematical concept in various real-world scenarios. Remember to focus on both the numerator and denominator, and utilize the methods described to avoid common misconceptions. With practice and a clear understanding of these principles, comparing fractions will become second nature.
Latest Posts
Latest Posts
-
What Will Not Increase The Strength Of An Electromagnet
May 11, 2025
-
What Is 64 Divided By 8
May 11, 2025
-
Is Heat And Temperature The Same Thing
May 11, 2025
-
Animals Who Eat Both Plants And Animals
May 11, 2025
-
What Happens To Blue Litmus Paper In Acid
May 11, 2025
Related Post
Thank you for visiting our website which covers about Is 1 8 Greater Than 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.