Is 1 7 A Rational Number
Juapaving
May 12, 2025 · 5 min read
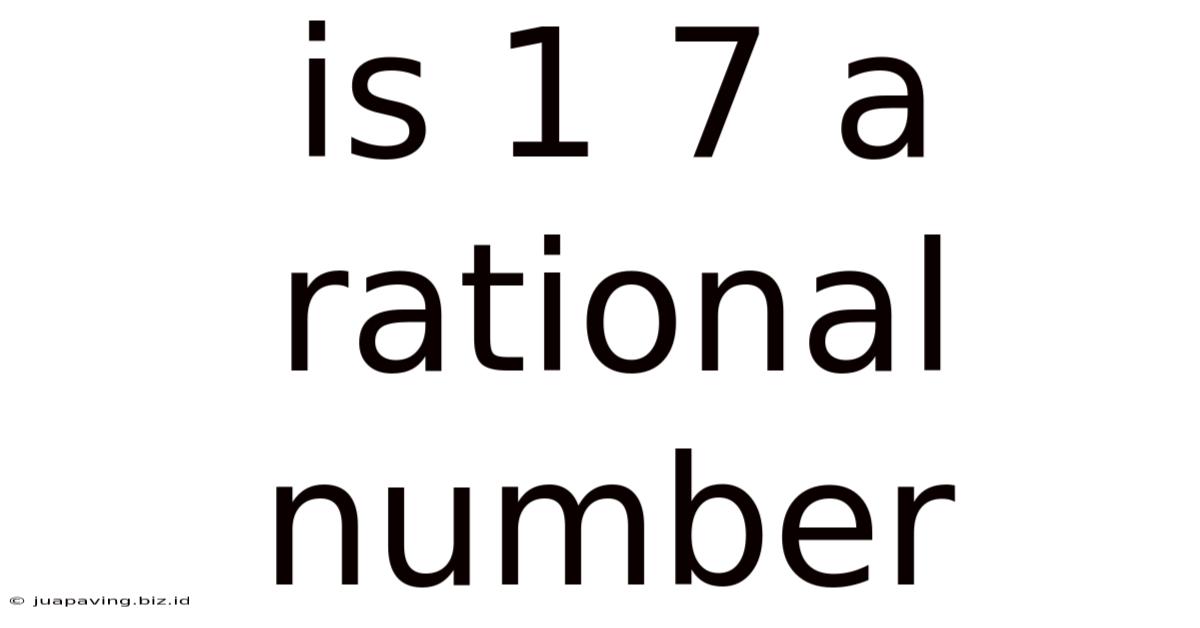
Table of Contents
Is 1/7 a Rational Number? A Deep Dive into Rational and Irrational Numbers
The question, "Is 1/7 a rational number?" might seem simple at first glance. However, understanding the answer requires a solid grasp of the definitions of rational and irrational numbers. This article will not only answer this specific question definitively but also explore the broader concepts of rational and irrational numbers, providing a comprehensive understanding of their properties and differences. We will also delve into how to identify rational numbers and dispel some common misconceptions.
Understanding Rational Numbers
A rational number is any number that can be expressed as a fraction p/q, where p and q are integers, and q is not equal to zero. This seemingly simple definition holds immense mathematical significance. The key characteristics are:
- Integers: Both the numerator (p) and the denominator (q) must be integers. Integers include whole numbers (like 0, 1, 2, 3...) and their negative counterparts (-1, -2, -3...).
- Non-zero denominator: The denominator (q) cannot be zero. Division by zero is undefined in mathematics.
Examples of rational numbers include:
- 1/2: Both 1 and 2 are integers.
- -3/4: Both -3 and 4 are integers.
- 5: This can be expressed as 5/1, where both 5 and 1 are integers. All whole numbers are rational numbers.
- 0.75: This can be expressed as 3/4.
- -2.2: This can be expressed as -11/5.
Notice a pattern? Rational numbers, when expressed as decimals, either terminate (end) or repeat in a predictable pattern. This is a crucial characteristic we'll revisit later.
Understanding Irrational Numbers
In contrast to rational numbers, irrational numbers cannot be expressed as a fraction p/q, where p and q are integers, and q is not zero. Their decimal representations are non-terminating and non-repeating. This means the decimal goes on forever without ever settling into a repeating pattern.
Famous examples of irrational numbers include:
- π (pi): The ratio of a circle's circumference to its diameter, approximately 3.14159..., continues infinitely without repeating.
- √2 (the square root of 2): This number, approximately 1.41421..., also has a non-terminating, non-repeating decimal expansion.
- e (Euler's number): The base of the natural logarithm, approximately 2.71828..., is another example of an irrational number.
- The golden ratio (φ): Approximately 1.61803..., is an irrational number with significant appearances in mathematics, art, and nature.
Is 1/7 a Rational Number? The Definitive Answer
Now, let's address the central question: Is 1/7 a rational number?
Yes, 1/7 is a rational number.
It perfectly fits the definition. Both 1 and 7 are integers, and the denominator (7) is not zero. Therefore, it satisfies the criteria for being a rational number.
While the decimal representation of 1/7 (0.142857142857...) might appear complex at first, it's crucial to understand that the sequence "142857" repeats infinitely. This repeating decimal pattern is a characteristic of rational numbers, solidifying its classification as rational.
Common Misconceptions about Rational Numbers
Several misconceptions often surround rational numbers. Let's address some of them:
-
Misconception 1: Long decimal numbers are always irrational. While irrational numbers have infinitely long non-repeating decimal expansions, many rational numbers also have long decimal expansions. The key difference lies in the repeating nature of the decimal expansion. A long decimal that repeats is rational; a long decimal that doesn't repeat is irrational.
-
Misconception 2: All fractions are rational. This is generally true. However, it's crucial to remember that both the numerator and denominator must be integers. For example, while √2/2 looks like a fraction, it's not a rational number because √2 is irrational.
-
Misconception 3: Recurring decimals are always irrational. This is incorrect. Recurring or repeating decimals are a hallmark of rational numbers. The repetition indicates a pattern that can be expressed as a fraction.
Identifying Rational Numbers: A Practical Approach
Determining whether a number is rational often involves these steps:
-
Check for integer representation: Can the number be expressed as a fraction where both the numerator and denominator are integers and the denominator is non-zero? If yes, it's rational.
-
Examine the decimal representation: Does the decimal terminate (end) or does it repeat in a predictable pattern? If either is true, the number is rational.
-
Convert recurring decimals to fractions: There are methods to convert repeating decimals into fractions, confirming their rational nature. For instance, 0.333... can be converted to 1/3.
The Significance of Rational and Irrational Numbers
The distinction between rational and irrational numbers is fundamental to various branches of mathematics:
- Algebra: Understanding rational numbers is crucial for solving equations and inequalities.
- Calculus: The concepts of limits and continuity heavily rely on the properties of rational and irrational numbers.
- Geometry: Irrational numbers like π and √2 are essential in calculating areas, volumes, and other geometric properties.
- Number Theory: A significant part of number theory is dedicated to studying the properties and relationships between rational and irrational numbers.
Conclusion: 1/7 and the World of Numbers
We've conclusively shown that 1/7 is a rational number because it meets all the criteria: it can be expressed as a fraction of two integers, and its decimal representation, while seemingly complex, ultimately repeats. Understanding the difference between rational and irrational numbers is crucial for grasping core mathematical concepts and their applications across numerous fields. The seemingly simple question of whether 1/7 is rational has opened a doorway to a deeper appreciation of the rich and intricate world of numbers. By mastering the concepts discussed here, you can confidently identify rational and irrational numbers and apply this knowledge in various mathematical contexts. Remember the key characteristics: integers for the numerator and denominator (excluding zero for the denominator), terminating decimals, and repeating decimals as indicators of rational numbers. Non-terminating, non-repeating decimals signify irrationality.
Latest Posts
Latest Posts
-
Functions And Parts Of A Microscope
May 12, 2025
-
Why Is Dna Replication Considered Semiconservative
May 12, 2025
-
5 Letter Words Ending With The
May 12, 2025
-
What Makes Something A Good Nucleophile
May 12, 2025
-
Round 0 40911 To The Nearest Whole Number
May 12, 2025
Related Post
Thank you for visiting our website which covers about Is 1 7 A Rational Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.