Is 1 5 Greater Than 1 3
Juapaving
May 11, 2025 · 5 min read
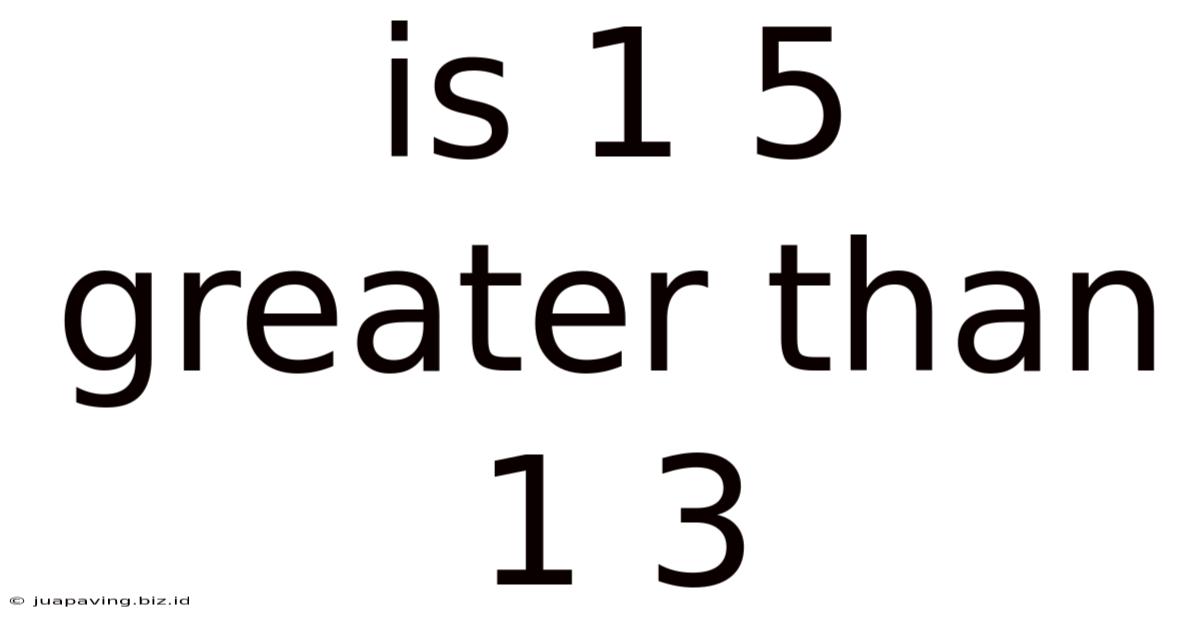
Table of Contents
Is 1/5 Greater Than 1/3? Understanding Fractions and Comparisons
Determining whether 1/5 is greater than 1/3 involves understanding the fundamental concepts of fractions and how to compare them. While it might seem simple at first glance, grasping the underlying principles is crucial for more advanced mathematical operations. This article will delve deep into this seemingly straightforward comparison, exploring various methods and providing a comprehensive understanding of fraction comparison.
Understanding Fractions: A Quick Refresher
A fraction represents a part of a whole. It's composed of two key elements:
- Numerator: The top number, indicating how many parts are being considered.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
In our case, we're comparing 1/5 and 1/3. 1/5 means one out of five equal parts, while 1/3 signifies one out of three equal parts. Visually, imagine a pie cut into five slices (1/5) and another pie cut into three slices (1/3). Which slice is larger?
Method 1: Visual Representation
A simple and intuitive way to compare fractions is through visual aids. Imagine two identical bars or circles. Divide one into five equal parts and shade one part. Divide the other into three equal parts and shade one part. By visually comparing the shaded areas, it's clear that the shaded portion in the bar divided into three parts (1/3) is larger than the shaded portion in the bar divided into five parts (1/5).
This method is particularly helpful for beginners as it provides a concrete representation of the fractions, making the comparison more easily understandable. However, it's less practical for comparing more complex fractions.
Method 2: Finding a Common Denominator
A more mathematically rigorous method involves finding theLeast Common Denominator (LCD). The LCD is the smallest number that is a multiple of both denominators. In our case, the denominators are 5 and 3. The multiples of 5 are 5, 10, 15, 20... and the multiples of 3 are 3, 6, 9, 12, 15... The smallest number common to both lists is 15.
Now, we convert both fractions to have a denominator of 15:
- 1/3: To get a denominator of 15, we multiply both the numerator and denominator by 5: (1 x 5) / (3 x 5) = 5/15
- 1/5: To get a denominator of 15, we multiply both the numerator and denominator by 3: (1 x 3) / (5 x 3) = 3/15
Now the comparison is straightforward: 5/15 is greater than 3/15. Therefore, 1/3 is greater than 1/5.
This method is reliable and works for all fractions, making it a preferred method for more complex fraction comparisons. The process of finding the LCD might require some prime factorization knowledge for larger numbers, but the principle remains the same.
Method 3: Using Decimals
Converting fractions to decimals provides another approach to comparison. To convert a fraction to a decimal, simply divide the numerator by the denominator:
- 1/3 = 0.333... (a repeating decimal)
- 1/5 = 0.2
By comparing the decimal values, it's evident that 0.333... is greater than 0.2. Therefore, 1/3 is greater than 1/5.
This method is particularly useful when dealing with fractions that are easily convertible to terminating decimals. However, it's less precise when dealing with repeating decimals, as you might need to consider the infinite sequence of digits for accurate comparison.
Method 4: Cross-Multiplication
Cross-multiplication offers a quick method for comparing two fractions. To compare a/b and c/d, we cross-multiply:
- If ad > bc, then a/b > c/d
- If ad < bc, then a/b < c/d
- If ad = bc, then a/b = c/d
Let's apply this to our fractions:
- 1/3 and 1/5
- Cross-multiply: (1 x 5) and (1 x 3) This gives us 5 and 3.
- Since 5 > 3, then 1/3 > 1/5
This method is efficient and avoids the need to find a common denominator, making it a popular choice for quick comparisons. However, it's crucial to remember the order of multiplication to avoid errors.
Beyond the Basics: Extending the Understanding
The comparison of 1/3 and 1/5 serves as a foundational stepping stone for understanding more complex fraction operations. The principles learned here are applicable to:
- Adding and Subtracting Fractions: Finding a common denominator is essential for these operations.
- Multiplying and Dividing Fractions: Understanding the relationship between numerators and denominators is key.
- Solving Equations with Fractions: Fraction comparison plays a crucial role in determining the solution.
- Working with Mixed Numbers: Mixed numbers (a combination of a whole number and a fraction) require similar comparison techniques.
- Understanding Percentages and Ratios: Fractions form the basis of these concepts.
Real-World Applications: Where Fraction Comparison Matters
The ability to compare fractions is not limited to mathematical exercises; it has numerous real-world applications:
- Cooking and Baking: Following recipes often requires precise measurements, demanding accurate fraction comparisons.
- Construction and Engineering: Accurate measurements and calculations are essential, utilizing fraction comparisons for precise constructions.
- Finance and Budgeting: Dealing with percentages, interest rates, and proportions involves working with fractions.
- Data Analysis: Interpreting data often involves comparing proportions and fractions.
- Science and Technology: Many scientific calculations and measurements rely on fraction comparisons.
Conclusion: Mastering Fraction Comparison
Determining whether 1/5 is greater than 1/3 highlights the importance of understanding fundamental fraction concepts. While visual representation offers an intuitive approach, methods like finding a common denominator, using decimals, and cross-multiplication provide more robust and reliable solutions for comparing fractions of all types. Mastering these techniques is crucial for success in various mathematical and real-world applications. The ability to confidently and accurately compare fractions is a cornerstone of numerical literacy and problem-solving skills, applicable far beyond the classroom. Continue practicing these methods to build a strong foundation in fraction understanding. Remember, consistent practice is key to mastering these essential mathematical skills.
Latest Posts
Latest Posts
-
Which Quadrilaterals Have Diagonals That Are Perpendicular
May 12, 2025
-
Molar Mass Of Iron Iii Hydroxide
May 12, 2025
-
In Dna Which Nitrogenous Base Pairs With Adenine
May 12, 2025
-
Where Are The Neutrons Located In The Atom
May 12, 2025
-
Awesome Words That Start With X
May 12, 2025
Related Post
Thank you for visiting our website which covers about Is 1 5 Greater Than 1 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.