Is 1 3 Bigger Than 3 4
Juapaving
May 14, 2025 · 5 min read
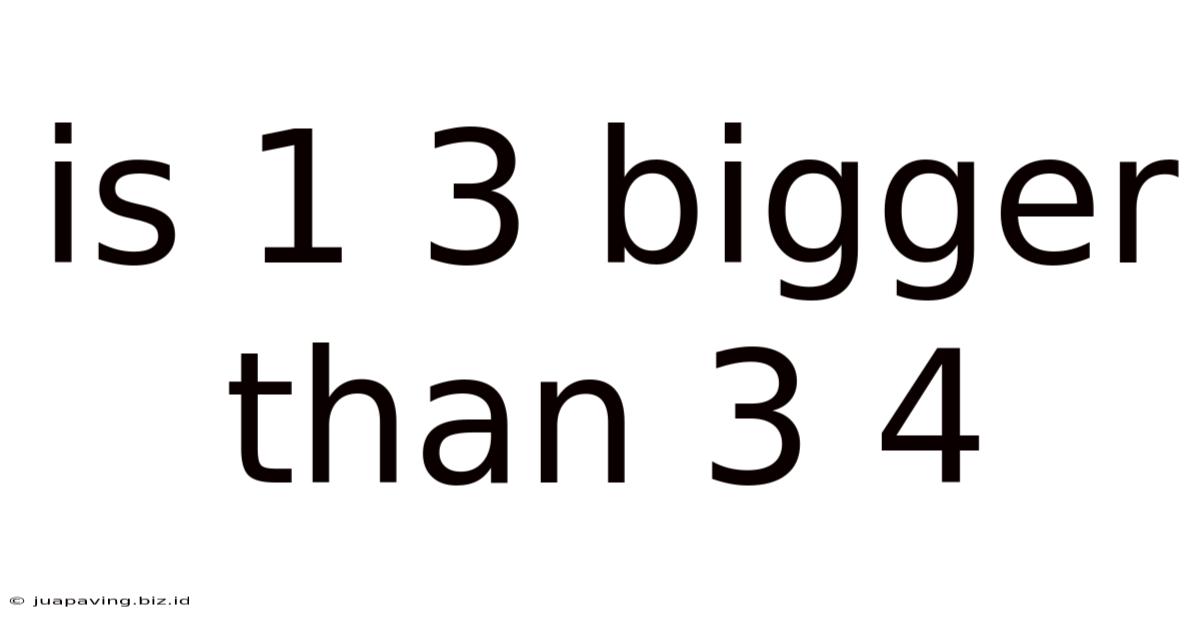
Table of Contents
Is 1/3 Bigger Than 3/4? A Deep Dive into Fraction Comparison
The question, "Is 1/3 bigger than 3/4?" might seem simple at first glance. However, a thorough understanding of fractions and their comparison is crucial for mastering basic arithmetic and tackling more complex mathematical concepts. This article will not only answer this specific question but also delve into the various methods for comparing fractions, offering a comprehensive guide for students and anyone looking to refresh their understanding of fractional arithmetic.
Understanding Fractions
Before we tackle the comparison, let's solidify our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates the total number of equal parts the whole is divided into, while the numerator shows how many of those parts are being considered.
For example, in the fraction 1/3, the denominator (3) means the whole is divided into three equal parts, and the numerator (1) means we're considering one of those parts. Similarly, 3/4 means the whole is divided into four equal parts, and we're considering three of them.
Methods for Comparing Fractions
Several methods exist for comparing fractions. Let's explore the most common and effective ones:
1. Finding a Common Denominator
This is perhaps the most straightforward method. To compare fractions using this method, we find a common multiple of the denominators – a number that both denominators can divide into evenly. Then, we convert both fractions to equivalent fractions with this common denominator. The fraction with the larger numerator is the larger fraction.
Let's apply this to our original question: Is 1/3 bigger than 3/4?
-
Find a common denominator: The least common multiple (LCM) of 3 and 4 is 12.
-
Convert the fractions:
- 1/3 = (1 x 4) / (3 x 4) = 4/12
- 3/4 = (3 x 3) / (4 x 3) = 9/12
-
Compare the numerators: Since 9 > 4, we can conclude that 9/12 (or 3/4) is greater than 4/12 (or 1/3).
Therefore, 1/3 is NOT bigger than 3/4; 3/4 is bigger than 1/3.
2. Converting to Decimals
Another effective method involves converting the fractions into decimals. This allows for a direct numerical comparison. To convert a fraction to a decimal, simply divide the numerator by the denominator.
- 1/3 = 0.333... (a repeating decimal)
- 3/4 = 0.75
By comparing the decimal values, it's clear that 0.75 (3/4) is larger than 0.333... (1/3).
Again, we confirm that 3/4 is bigger than 1/3.
3. Visual Representation
Visual aids can be incredibly helpful, especially for beginners. Imagine two identical circles. Divide one circle into three equal parts and shade one part (representing 1/3). Divide the other circle into four equal parts and shade three parts (representing 3/4). A visual comparison clearly shows that the shaded area in the second circle (3/4) is significantly larger than the shaded area in the first circle (1/3).
4. Cross-Multiplication
This method is a shortcut for comparing two fractions. Cross-multiply the numerators and denominators. The fraction with the larger product is the larger fraction.
-
Cross-multiply:
- 1/3 and 3/4
- (1 x 4) = 4
- (3 x 3) = 9
-
Compare the products: Since 9 > 4, we conclude that 3/4 is greater than 1/3.
Beyond the Basics: Working with Mixed Numbers and Improper Fractions
The methods discussed above also apply to mixed numbers (a whole number and a fraction, like 2 1/2) and improper fractions (where the numerator is greater than or equal to the denominator, like 7/4). However, it's often helpful to convert mixed numbers and improper fractions into either improper fractions or decimals before comparison.
For example, to compare 2 1/3 and 5/2:
-
Convert to improper fractions:
- 2 1/3 = (2 x 3 + 1) / 3 = 7/3
- 5/2 remains as 5/2
-
Find a common denominator: The LCM of 3 and 2 is 6.
-
Convert to equivalent fractions:
- 7/3 = (7 x 2) / (3 x 2) = 14/6
- 5/2 = (5 x 3) / (2 x 3) = 15/6
-
Compare: 15/6 > 14/6, therefore 5/2 > 2 1/3
Real-World Applications of Fraction Comparison
Understanding fraction comparison isn't just an academic exercise; it has practical applications in various aspects of daily life:
-
Cooking and Baking: Recipes often require precise measurements using fractions. Knowing how to compare fractions ensures accurate ingredient proportions.
-
Construction and Engineering: Precise measurements and calculations involving fractions are crucial in construction and engineering projects.
-
Finance: Understanding fractions is essential for managing budgets, calculating interest rates, and understanding financial statements.
-
Data Analysis: Interpreting data often involves working with fractions and percentages, requiring the ability to compare fractional values.
Conclusion: Mastering Fraction Comparison for Mathematical Proficiency
Comparing fractions is a fundamental skill in mathematics. By understanding the various methods outlined in this article – finding a common denominator, converting to decimals, visual representation, and cross-multiplication – you can confidently tackle fraction comparison problems. This skill isn't just about solving mathematical problems; it's a building block for more advanced mathematical concepts and a crucial skill for navigating various aspects of daily life. Regular practice and a clear understanding of the underlying principles are key to mastering this essential skill. Remember to choose the method that feels most comfortable and efficient for you, and don't hesitate to utilize visual aids to reinforce your understanding. The ability to accurately compare fractions is a testament to a strong foundation in mathematical reasoning.
Latest Posts
Latest Posts
-
Letter For Authorization To Collect Documents
May 14, 2025
-
How Many Feet In 25 Inches
May 14, 2025
-
5 3 And A Half In Cm
May 14, 2025
-
How Is Buoyancy And Density Related
May 14, 2025
-
Is Heat Capacity Intensive Or Extensive
May 14, 2025
Related Post
Thank you for visiting our website which covers about Is 1 3 Bigger Than 3 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.