Is 1 3 Bigger Than 1 4
Juapaving
May 14, 2025 · 5 min read
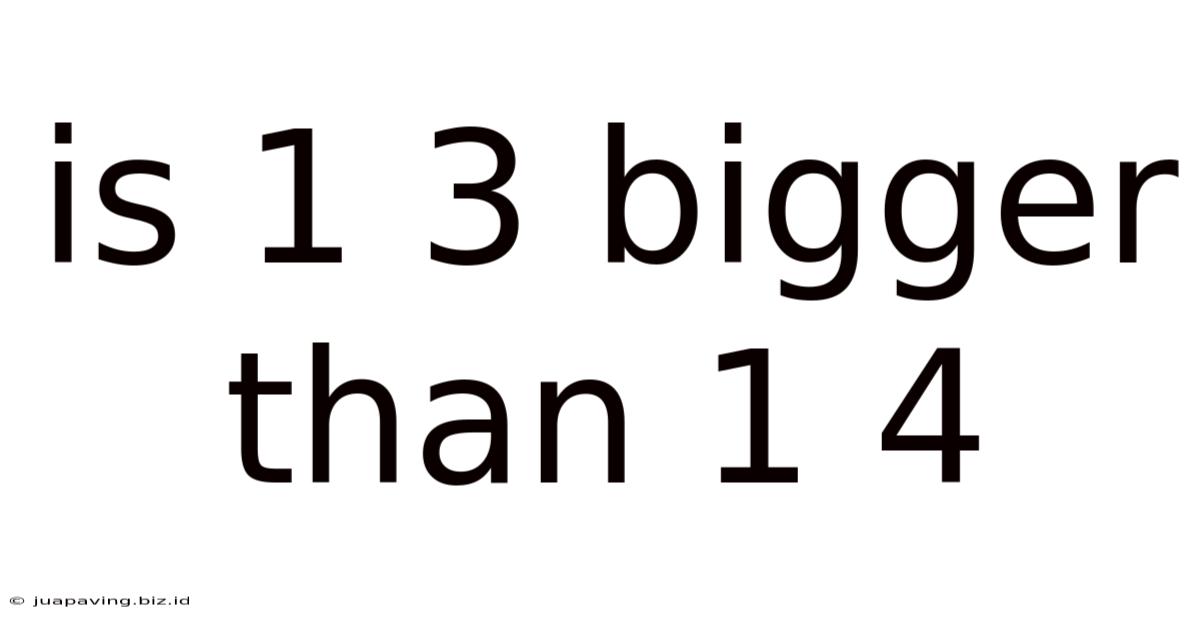
Table of Contents
Is 1/3 Bigger Than 1/4? A Deep Dive into Fraction Comparison
The question, "Is 1/3 bigger than 1/4?" seems deceptively simple. It's the kind of question that pops up in elementary school math classes, yet understanding the underlying principles can lay a solid foundation for more complex mathematical concepts. This article will not only answer this question definitively but will also explore various methods for comparing fractions, highlighting the importance of understanding fractional relationships.
Understanding Fractions: Parts of a Whole
Before we dive into comparing 1/3 and 1/4, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's written as a numerator (the top number) over a denominator (the bottom number). The numerator indicates how many parts you have, while the denominator indicates how many equal parts the whole is divided into.
For example, in the fraction 1/3, the numerator is 1, and the denominator is 3. This means we have 1 part out of a whole that's divided into 3 equal parts. Similarly, 1/4 represents 1 part out of a whole divided into 4 equal parts.
Visualizing Fractions: The Power of Representation
Visual aids are incredibly helpful when comparing fractions. Imagine two identical pizzas. Cut the first pizza into 3 equal slices and the second into 4 equal slices.
- Pizza 1 (1/3): You take one slice. You have 1/3 of the pizza.
- Pizza 2 (1/4): You take one slice. You have 1/4 of the pizza.
Which slice is bigger? The slice from the pizza cut into 3 pieces (1/3) is clearly larger than the slice from the pizza cut into 4 pieces (1/4). This visual representation immediately demonstrates that 1/3 is bigger than 1/4.
Comparing Fractions: Three Effective Methods
While visualization is helpful, it's not always practical for more complex fractions. Here are three reliable methods for comparing fractions:
1. Finding a Common Denominator
This is a classic and widely used method. To compare fractions, we need to express them with the same denominator. The least common multiple (LCM) of the denominators is the most efficient common denominator to use.
-
Finding the LCM of 3 and 4: The multiples of 3 are 3, 6, 9, 12, 15... The multiples of 4 are 4, 8, 12, 16... The least common multiple is 12.
-
Converting the fractions:
- 1/3 = (1 x 4) / (3 x 4) = 4/12
- 1/4 = (1 x 3) / (4 x 3) = 3/12
Now we can easily compare: 4/12 is greater than 3/12. Therefore, 1/3 is bigger than 1/4.
2. Cross-Multiplication
This method is a shortcut for comparing fractions. We cross-multiply the numerators and denominators.
-
Cross-multiply: (1 x 4) = 4 and (1 x 3) = 3
-
Compare the results: Since 4 > 3, 1/3 is bigger than 1/4.
3. Decimal Conversion
Converting fractions to decimals provides another way to compare them.
-
Converting to decimals:
- 1/3 = 0.333... (a repeating decimal)
- 1/4 = 0.25
-
Comparing decimals: 0.333... > 0.25. Therefore, 1/3 is bigger than 1/4.
Beyond the Basics: Understanding the Relationship
The comparison of 1/3 and 1/4 illustrates a broader principle: For fractions with the same numerator, the fraction with the smaller denominator is the larger fraction. This is because a smaller denominator means the whole is divided into fewer parts, making each part larger.
Think about it this way: if you divide a cake into 3 slices, each slice is bigger than if you divide the same cake into 4 slices.
Real-World Applications: Fractions in Everyday Life
Understanding fractions isn't just an academic exercise; it's crucial for navigating everyday life. Here are some examples:
- Cooking and Baking: Recipes often involve fractions (1/2 cup of sugar, 1/4 teaspoon of salt). Accurate measurements are essential for successful cooking.
- Shopping: Sales and discounts are frequently expressed as fractions (1/3 off, 25% off, which is equivalent to 1/4 off).
- Construction and Engineering: Precise measurements and calculations involving fractions are fundamental in these fields.
- Finance: Understanding fractions is essential for managing budgets, calculating interest rates, and analyzing financial statements.
Expanding Knowledge: Further Exploration of Fractions
Mastering fraction comparison opens doors to more complex mathematical concepts:
- Improper Fractions and Mixed Numbers: Learn to convert between improper fractions (where the numerator is larger than the denominator) and mixed numbers (a whole number and a fraction).
- Adding, Subtracting, Multiplying, and Dividing Fractions: Build upon your understanding of fraction comparison to perform arithmetic operations on fractions.
- Ratios and Proportions: Understand the relationship between fractions and ratios, which are used to compare quantities.
- Percentages: Learn to convert fractions to percentages and vice-versa, essential for understanding data and statistics.
Conclusion: Mastering Fractions for a Brighter Future
The seemingly simple question, "Is 1/3 bigger than 1/4?" serves as a gateway to a deeper understanding of fractions. By exploring different methods for comparing fractions and understanding their real-world applications, you build a solid mathematical foundation for future learning and problem-solving. Whether you're a student, a professional, or simply someone curious about the world of numbers, grasping the intricacies of fractions is a valuable skill that will benefit you in countless ways. Remember to practice regularly and use various methods to reinforce your understanding. The more you practice, the more confident and proficient you’ll become in working with fractions.
Latest Posts
Latest Posts
-
Number In Words From 1 To 100
May 14, 2025
-
What Is 96 Inches In Feet
May 14, 2025
-
What Percentage Is 35 Out Of 40
May 14, 2025
-
Electricity Is Measured In What Unit
May 14, 2025
-
Is A Pencil A Conductor Or Insulator
May 14, 2025
Related Post
Thank you for visiting our website which covers about Is 1 3 Bigger Than 1 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.