Is 1 3 A Rational Number
Juapaving
May 13, 2025 · 5 min read
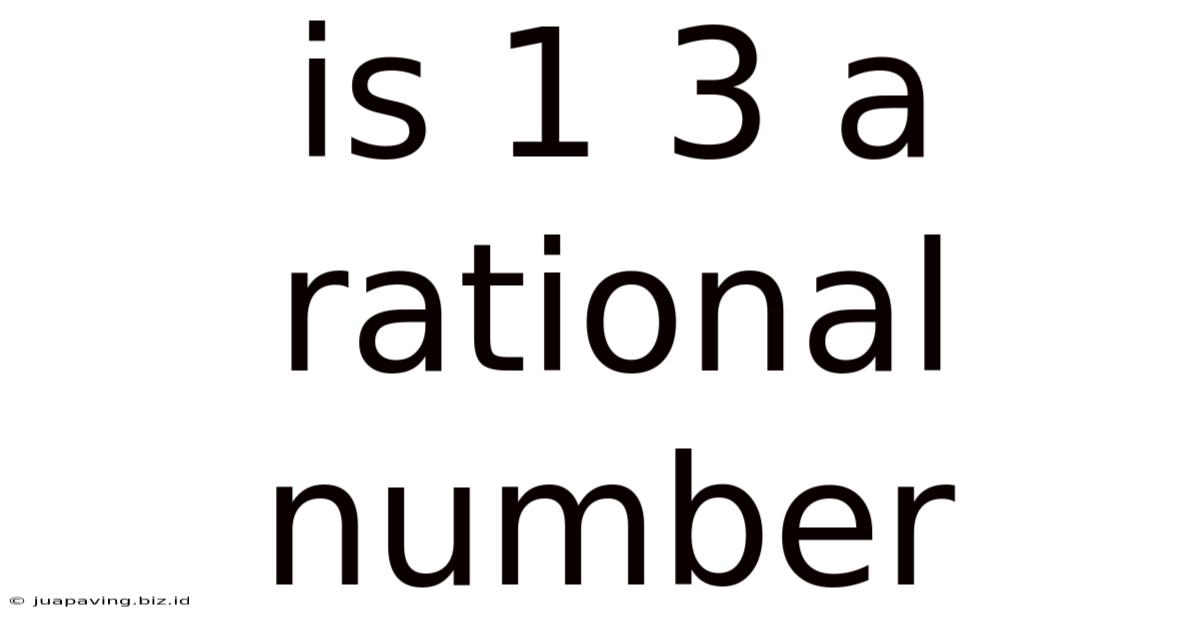
Table of Contents
Is 1/3 a Rational Number? A Deep Dive into Rational and Irrational Numbers
The question, "Is 1/3 a rational number?" might seem trivial at first glance. However, understanding the answer requires a deeper exploration of what constitutes a rational number and how it differs from its irrational counterpart. This article will not only definitively answer the question but also provide a comprehensive overview of rational and irrational numbers, exploring their properties and significance in mathematics.
Understanding Rational Numbers
A rational number is any number that can be expressed as the quotient or fraction p/q of two integers, where p is the numerator and q is the non-zero denominator. The key here is the ability to represent the number as a simple fraction. This fraction can be positive, negative, or zero.
Examples of Rational Numbers:
- 1/2: This is a classic example. One divided by two equals 0.5.
- -3/4: Negative rational numbers are also included.
- 5: Any integer can be expressed as a rational number (e.g., 5/1).
- 0: Zero is a rational number (e.g., 0/1).
- 0.75: Decimals that terminate (end) are rational because they can be expressed as fractions (0.75 = 3/4).
- 0.333... (repeating decimal): Even repeating decimals are rational. We'll explore this in more detail later.
Understanding Irrational Numbers
An irrational number, on the other hand, cannot be expressed as a fraction p/q, where p and q are integers and q is not zero. These numbers have decimal representations that neither terminate nor repeat. They extend infinitely without any discernible pattern.
Examples of Irrational Numbers:
- π (pi): The ratio of a circle's circumference to its diameter, approximately 3.14159..., continues infinitely without repeating.
- √2 (the square root of 2): This number cannot be expressed as a simple fraction. Its decimal representation is approximately 1.414213..., and it continues infinitely without repeating.
- e (Euler's number): The base of the natural logarithm, approximately 2.71828..., is another famous irrational number.
- φ (the golden ratio): Approximately 1.61803..., also has an infinite non-repeating decimal representation.
Decimals: A Bridge Between Rational and Irrational Numbers
The decimal representation of a number offers a clear way to distinguish between rational and irrational numbers.
-
Rational numbers: Have decimal representations that either terminate (end) or repeat in a predictable pattern. For example:
- 1/4 = 0.25 (terminating)
- 1/3 = 0.333... (repeating)
- 1/7 = 0.142857142857... (repeating)
-
Irrational numbers: Have decimal representations that are both non-terminating and non-repeating. Their digits continue infinitely without any repeating pattern.
Proving 1/3 is Rational
Now, let's definitively answer the central question: Is 1/3 a rational number?
The answer is a resounding yes. 1/3 perfectly fits the definition of a rational number. It's expressed as a fraction where:
- p = 1 (an integer)
- q = 3 (an integer, and importantly, not zero)
Therefore, 1/3 satisfies the criteria for a rational number.
Furthermore, its decimal representation, 0.333..., is a repeating decimal. While it doesn't terminate, the repetition of the digit "3" confirms its rational nature. This repeating decimal can be expressed as a fraction, solidifying its status as a rational number.
Converting Repeating Decimals to Fractions
The ability to convert a repeating decimal to a fraction provides further evidence that 1/3 is rational. Let's illustrate the process:
Let x = 0.333...
Multiply both sides by 10:
10x = 3.333...
Subtract the first equation from the second equation:
10x - x = 3.333... - 0.333...
9x = 3
x = 3/9
Simplifying the fraction:
x = 1/3
This proves that the repeating decimal 0.333..., which is the decimal representation of 1/3, can be expressed as a fraction, further confirming its rationality.
The Significance of Rational and Irrational Numbers
The distinction between rational and irrational numbers is fundamental in mathematics. They form the building blocks of the real number system, which encompasses all numbers on the number line.
Rational numbers are essential for everyday calculations, measurements, and practical applications. Irrational numbers, while seemingly more abstract, are crucial in various mathematical fields, including geometry (π), calculus (e), and number theory. Understanding their properties is vital for advancing mathematical knowledge and solving complex problems.
Real-World Applications: Why Understanding Rational Numbers Matters
The practical applications of rational numbers are vast and impact many aspects of our lives:
-
Measurement and Engineering: Rational numbers are indispensable in engineering and construction. Precise measurements of lengths, areas, and volumes are crucial, and these measurements are often expressed as fractions or decimals representing rational numbers. Building a bridge, designing a circuit board, or constructing a building all rely on the accurate application of rational numbers.
-
Finance and Accounting: Financial transactions involve precise calculations with money, percentages, and interest rates. All these calculations rely heavily on rational numbers. Accounting relies on balanced budgets and precise financial statements, which necessitate the use of rational numbers.
-
Cooking and Baking: Recipes often use fractions to specify ingredient quantities, ensuring consistent results. The accurate measurement of ingredients, such as 1/2 cup of flour or 1/4 teaspoon of salt, relies on an understanding of rational numbers.
-
Computer Science: While computers primarily work with binary numbers (0 and 1), they ultimately represent and manipulate rational numbers in various applications, including graphical displays, simulations, and data analysis.
-
Data Analysis and Statistics: Data analysis often involves calculating averages, proportions, and probabilities, which frequently rely on rational numbers. Statistics depends heavily on the accurate interpretation of rational numbers to make informed decisions based on data.
Conclusion: 1/3 is undeniably Rational
In conclusion, the question, "Is 1/3 a rational number?" has been definitively answered. 1/3 is a rational number because it can be expressed as the fraction 1/3, where both the numerator and denominator are integers, and the denominator is non-zero. Its repeating decimal representation further solidifies this classification. Understanding the fundamental difference between rational and irrational numbers is crucial for grasping core mathematical concepts and applying them effectively in various fields. This article aims to provide a clear and comprehensive understanding of these number types and their importance in the world around us. The ability to identify and work with rational and irrational numbers is essential for problem-solving across numerous disciplines.
Latest Posts
Latest Posts
-
Tortoise And The Hare Moral Of The Story
May 14, 2025
-
2 Hours Is How Many Seconds
May 14, 2025
-
Five Letter Words Starting With Dan
May 14, 2025
-
5 Letter Word Starting With Ray
May 14, 2025
-
Diagram Of The Ear With Labels
May 14, 2025
Related Post
Thank you for visiting our website which covers about Is 1 3 A Rational Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.