Is 1 2 Bigger Than 7 16
Juapaving
May 09, 2025 · 5 min read
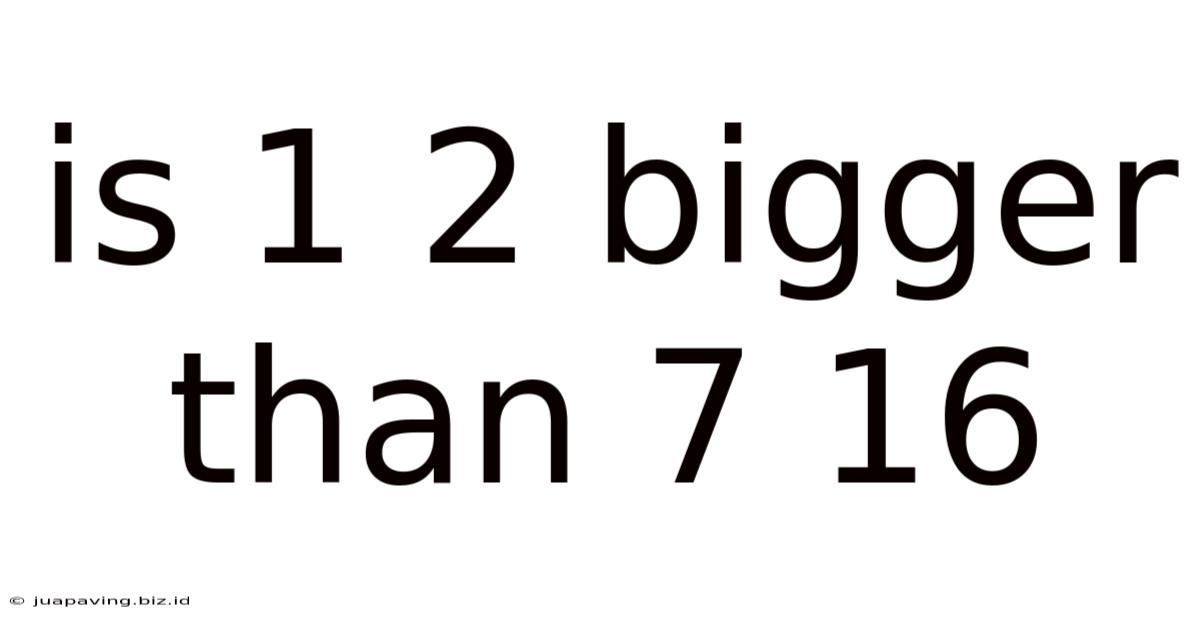
Table of Contents
Is 1/2 Bigger Than 7/16? A Deep Dive into Fraction Comparison
Comparing fractions can seem daunting, especially when they don't share a common denominator. This article will thoroughly explore the question: "Is 1/2 bigger than 7/16?" We'll not only answer this specific question but also equip you with the skills to compare any two fractions confidently. We'll delve into various methods, from finding common denominators to using decimal conversions and visualizing the fractions. By the end, you'll have a comprehensive understanding of fraction comparison and be able to tackle similar problems with ease.
Understanding Fractions: A Quick Refresher
Before jumping into the comparison, let's quickly review what fractions represent. A fraction is a part of a whole. It's expressed as a numerator (the top number) over a denominator (the bottom number). The numerator indicates how many parts you have, and the denominator indicates how many equal parts the whole is divided into.
For example, in the fraction 1/2, the numerator (1) represents one part, and the denominator (2) means the whole is divided into two equal parts. Therefore, 1/2 represents one-half of the whole.
Similarly, in the fraction 7/16, the numerator (7) represents seven parts, and the denominator (16) indicates the whole is divided into sixteen equal parts.
Method 1: Finding a Common Denominator
The most common method for comparing fractions is to find a common denominator. This means finding a number that is a multiple of both denominators. Once you have a common denominator, you can directly compare the numerators.
Let's apply this to our fractions, 1/2 and 7/16.
-
Find the least common multiple (LCM) of the denominators: The denominators are 2 and 16. The multiples of 2 are 2, 4, 6, 8, 10, 12, 14, 16... The multiples of 16 are 16, 32, 48... The least common multiple is 16.
-
Convert the fractions to equivalent fractions with the common denominator:
-
For 1/2, we multiply both the numerator and the denominator by 8 (because 16/2 = 8): (1 * 8) / (2 * 8) = 8/16
-
7/16 remains the same since it already has the denominator 16.
-
-
Compare the numerators: Now we compare 8/16 and 7/16. Since 8 > 7, we conclude that 8/16 > 7/16.
Therefore, 1/2 is bigger than 7/16.
Method 2: Converting to Decimals
Another effective method is to convert both fractions into decimals and then compare them. This method is particularly useful when dealing with more complex fractions or when you're more comfortable working with decimals.
-
Convert 1/2 to a decimal: Divide the numerator (1) by the denominator (2): 1 ÷ 2 = 0.5
-
Convert 7/16 to a decimal: Divide the numerator (7) by the denominator (16): 7 ÷ 16 = 0.4375
-
Compare the decimals: Since 0.5 > 0.4375, we conclude that 1/2 > 7/16.
Again, we confirm that 1/2 is bigger than 7/16.
Method 3: Visual Representation
Visualizing fractions can be a helpful approach, especially for beginners. You can represent fractions using diagrams, such as circles or rectangles, divided into equal parts.
Imagine two circles. Divide the first circle into two equal halves and shade one half. This represents 1/2. Now, divide the second circle into sixteen equal parts and shade seven of them. This represents 7/16. By visually comparing the shaded areas, you can easily see that the shaded area in the first circle (representing 1/2) is larger than the shaded area in the second circle (representing 7/16).
This visual representation reinforces the conclusion that 1/2 is bigger than 7/16.
Beyond the Comparison: Mastering Fraction Skills
Understanding the comparison between 1/2 and 7/16 is just the beginning. Proficiency in working with fractions is crucial for various mathematical concepts and real-world applications. Here are some additional skills to build upon:
Adding and Subtracting Fractions: To add or subtract fractions, they must have a common denominator. Once they do, you add or subtract the numerators and keep the denominator the same.
Multiplying Fractions: Multiply the numerators together and the denominators together. Simplify the resulting fraction if possible.
Dividing Fractions: To divide fractions, invert the second fraction (the divisor) and then multiply.
Simplifying Fractions: Simplify fractions by dividing both the numerator and the denominator by their greatest common divisor (GCD). This reduces the fraction to its simplest form.
Real-World Applications of Fraction Comparison
Comparing fractions isn't just an abstract mathematical exercise; it has numerous real-world applications:
-
Cooking and Baking: Recipes often involve fractions, and understanding fraction comparisons is essential for accurate measurements and successful cooking.
-
Construction and Engineering: Precise measurements and calculations using fractions are critical in construction and engineering projects.
-
Finance and Budgeting: Understanding fractions is crucial for managing finances, calculating percentages, and interpreting financial data.
-
Data Analysis: Fractions are frequently used to represent proportions and ratios in data analysis and statistics.
Conclusion: Confidence in Fraction Comparison
This in-depth exploration of the comparison between 1/2 and 7/16 has not only answered the initial question but also equipped you with the tools and understanding to confidently compare any two fractions. By mastering the methods of finding common denominators, converting to decimals, and visualizing fractions, you can tackle various mathematical problems and real-world scenarios involving fractions with ease. Remember to practice regularly, and soon you'll find that comparing fractions becomes second nature. The key takeaway is to choose the method that you find most intuitive and efficient. Whether it's finding a common denominator, using decimals, or visual representation, the ultimate goal is accuracy and understanding. Keep practicing, and you will master the art of fraction comparison!
Latest Posts
Latest Posts
-
The Likelihood That A Particular Event Will Occur
May 09, 2025
-
What Is The Least Common Multiple Of 36 And 54
May 09, 2025
-
What Is The Function Of Rhizoids
May 09, 2025
-
Nucleolus In Plant Or Animal Cells
May 09, 2025
-
The Ratio Of Atoms In Hcl Is
May 09, 2025
Related Post
Thank you for visiting our website which covers about Is 1 2 Bigger Than 7 16 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.