Is 1 2 Bigger Than 1 8
Juapaving
May 09, 2025 · 5 min read
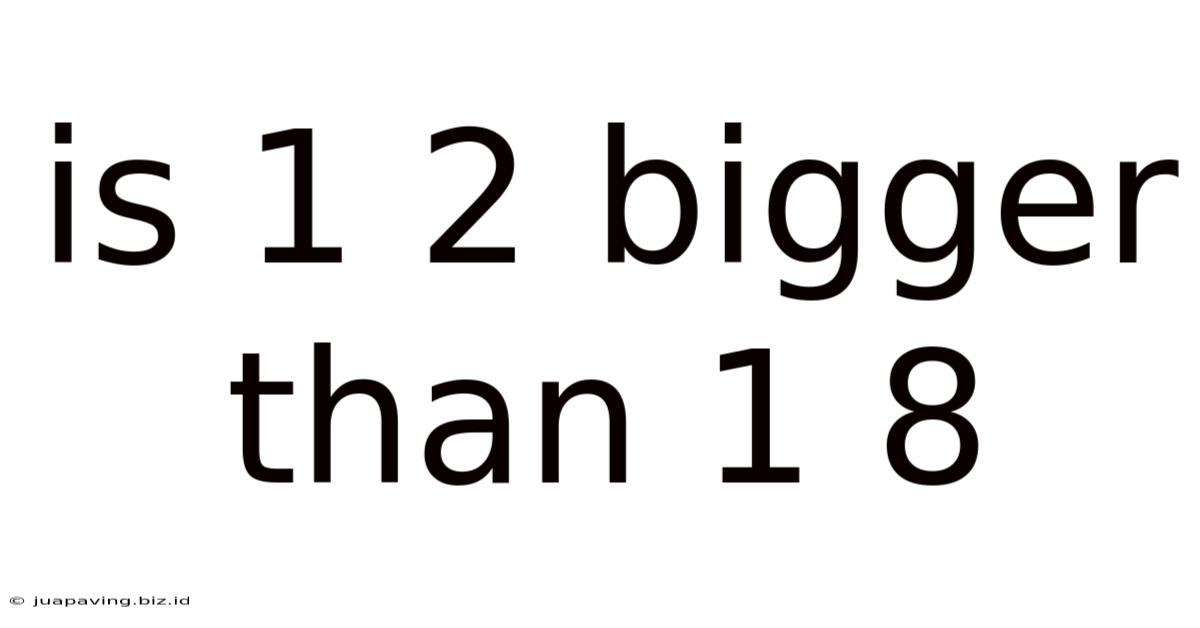
Table of Contents
Is 1/2 Bigger Than 1/8? A Deep Dive into Fraction Comparison
Understanding fractions is fundamental to mathematics and everyday life. Whether you're splitting a pizza, measuring ingredients for a recipe, or tackling complex equations, knowing how to compare fractions is crucial. This comprehensive guide will explore the question, "Is 1/2 bigger than 1/8?", providing various methods for comparing fractions and expanding on the broader concept of fraction comparison. We'll cover visual representations, numerical methods, and real-world applications, ensuring a thorough understanding of this essential mathematical skill.
Visualizing Fractions: The Pizza Analogy
One of the easiest ways to grasp the concept of fraction comparison is through visual aids. Imagine a pizza cut into equal slices.
1/2 of a Pizza:
If you have a pizza cut into two equal slices, 1/2 represents one of those two slices. This is a relatively large portion of the pizza.
1/8 of a Pizza:
Now imagine the same pizza cut into eight equal slices. 1/8 represents only one of those eight slices. This is a much smaller portion compared to 1/2.
Clearly, 1/2 of the pizza is significantly larger than 1/8. This visual representation makes the comparison intuitive and easy to understand.
Numerical Methods for Comparing Fractions
While visual aids are helpful for understanding the basic concept, numerical methods are necessary for more complex fraction comparisons. Here are several approaches:
Method 1: Finding a Common Denominator
This is the most common and reliable method for comparing fractions. The denominator represents the total number of equal parts, and the numerator represents the number of parts we're considering. To compare 1/2 and 1/8, we need to find a common denominator – a number that both 2 and 8 divide into evenly. In this case, the least common denominator (LCD) is 8.
-
Convert 1/2: To convert 1/2 to an equivalent fraction with a denominator of 8, we multiply both the numerator and the denominator by 4: (1 x 4) / (2 x 4) = 4/8.
-
Comparison: Now we can easily compare 4/8 and 1/8. Since 4 is greater than 1, 4/8 (which is equivalent to 1/2) is greater than 1/8.
Therefore, 1/2 > 1/8
Method 2: Converting to Decimals
Another way to compare fractions is to convert them to decimals. This method is particularly useful when dealing with fractions that don't share an easily found common denominator.
-
Convert 1/2 to a decimal: 1/2 = 0.5
-
Convert 1/8 to a decimal: 1/8 = 0.125
-
Comparison: Comparing the decimal values, 0.5 > 0.125.
Again, this confirms that 1/2 is greater than 1/8.
Method 3: Cross-Multiplication
This method is a quick way to compare two fractions without finding a common denominator. Cross-multiply the numerators and denominators:
-
Multiply the numerator of the first fraction (1/2) by the denominator of the second fraction (8): 1 x 8 = 8
-
Multiply the numerator of the second fraction (1/8) by the denominator of the first fraction (2): 1 x 2 = 2
-
Comparison: Since 8 > 2, the fraction 1/2 is greater than 1/8.
Understanding Fraction Size Intuitively
Beyond the mathematical methods, developing an intuitive understanding of fraction size is crucial. Consider these points:
-
The larger the denominator, the smaller the individual pieces: If you divide a pizza into more slices (larger denominator), each individual slice will be smaller.
-
The larger the numerator, the larger the portion: If you have more slices (larger numerator) of the same size, you have a larger portion of the whole.
-
Fractions with the same denominator are easily comparable: If two fractions have the same denominator, the fraction with the larger numerator is the larger fraction.
Real-World Applications of Fraction Comparison
Comparing fractions isn't just an abstract mathematical exercise. It has numerous real-world applications:
-
Cooking and Baking: Following recipes often involves precise measurements, requiring comparison of fractions. For example, deciding whether 1/2 cup of sugar is more or less than 1/8 cup.
-
Construction and Engineering: Accurate measurements are critical in construction and engineering, demanding precise comparison of fractional measurements.
-
Finance and Budgeting: Understanding fractions is essential for managing finances, comparing discounts, and understanding proportions of budgets.
-
Data Analysis: In data analysis and statistics, fractions and proportions are commonly used to represent and compare data sets.
Beyond 1/2 and 1/8: Expanding the Concept
The principle of comparing fractions extends far beyond the simple example of 1/2 and 1/8. The methods outlined above – finding a common denominator, converting to decimals, and cross-multiplication – can be applied to any two fractions, regardless of their complexity. For example, you can use these methods to compare fractions like 3/4 and 5/6, 7/12 and 2/3, or even fractions with larger numbers.
Addressing Potential Misconceptions
Some common misconceptions about fractions can lead to incorrect comparisons. It's essential to clarify these:
-
Larger Numerator Doesn't Always Mean Larger Fraction: A larger numerator doesn't automatically mean a larger fraction if the denominators are different. For example, 5/10 is smaller than 3/4 even though 5 > 3.
-
Visualizations Can Be Deceiving: While visual aids are helpful, they can be misleading if the slices aren't perfectly equal. Always rely on numerical methods for accurate comparison.
-
Incorrectly Simplifying Fractions: Ensure you correctly simplify fractions before comparison to avoid errors.
Conclusion: Mastering Fraction Comparison
Understanding how to compare fractions is a fundamental mathematical skill with widespread real-world applications. Whether you use visual aids, common denominators, decimal conversions, or cross-multiplication, the key is to choose a method that is comfortable and reliable for you. By mastering fraction comparison, you build a solid foundation for more advanced mathematical concepts and improve your ability to tackle everyday problems that involve fractions. Remember, practice is key to solidifying your understanding and increasing your confidence in working with fractions. The more you practice, the more intuitive and effortless fraction comparison will become. So grab a pizza, some measuring cups, or a workbook, and start practicing!
Latest Posts
Latest Posts
-
What Is A Pack Of Hyenas Called
May 09, 2025
-
Difference Between African Elephant And Indian Elephant
May 09, 2025
-
What Is The Name Of The Following Compound
May 09, 2025
-
What Is The Prime Factorization Of 735
May 09, 2025
-
The Unit For Energy Is The
May 09, 2025
Related Post
Thank you for visiting our website which covers about Is 1 2 Bigger Than 1 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.