If X 6 7 Then X Is Equal To
Juapaving
May 11, 2025 · 5 min read
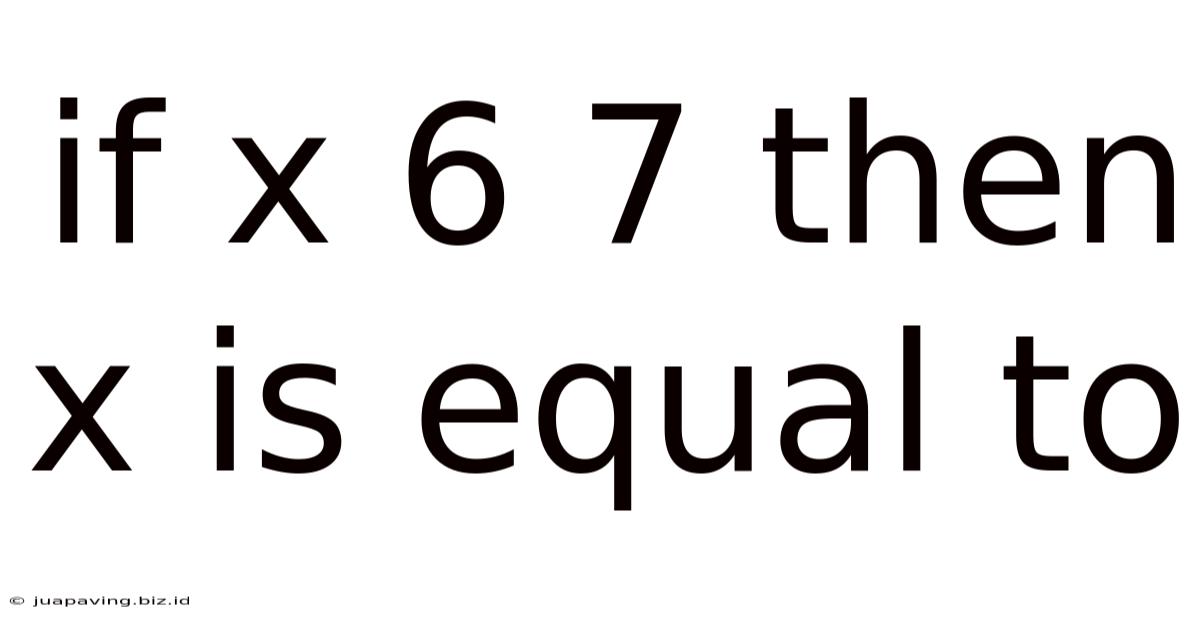
Table of Contents
If x⁶ = 7, Then x is Equal To: A Deep Dive into Solving Higher-Order Equations
Finding the solutions to the equation x⁶ = 7 might seem straightforward at first glance. However, delving into the intricacies reveals a richer mathematical landscape than initially apparent. This exploration will unravel the complexities of solving higher-order equations, examining the real and complex solutions, and touching upon the broader context of polynomial equations and their applications.
Understanding the Problem: Roots of Unity and the Fundamental Theorem of Algebra
The equation x⁶ = 7 is a sixth-degree polynomial equation. The Fundamental Theorem of Algebra dictates that a polynomial of degree n has exactly n roots (solutions), although some may be repeated. Therefore, our equation, x⁶ = 7, has six solutions.
To understand these solutions, we need to introduce the concept of roots of unity. A root of unity is a complex number that, when raised to a positive integer power, equals 1. These are crucial in understanding the solutions to equations of the form xⁿ = a, where 'a' is a complex number.
For our equation, we can rewrite it as:
x⁶ = 7 = 7 * (1)
This shows that we are looking for six numbers that, when multiplied by themselves six times, result in 7. The '1' here is crucial because it represents the principal root of unity (1 raised to any power remains 1).
Finding the Real Solutions
While we expect six solutions, let's start by looking for the real solutions. A real solution is a solution that is a real number (not imaginary or complex).
We can easily find one real solution by taking the sixth root of 7:
x = ⁷√7 ≈ 1.383
This is the principal sixth root of 7. It is a positive real number. However, remember that there are five other solutions!
Delving into the Complex Solutions
To find the remaining five solutions, we must venture into the realm of complex numbers. We can express the solutions using polar coordinates, employing Euler's formula:
e^(iθ) = cos(θ) + i sin(θ)
Where:
- 'i' is the imaginary unit (√-1)
- 'θ' is the angle in radians.
Let's represent 7 in polar form:
7 = 7 * e^(i * 0) (Since the angle for a positive real number is 0)
Now, we can express the solutions as:
xₖ = ⁷√7 * e^(i * (0 + 2πk)/6) where k = 0, 1, 2, 3, 4, 5
Let's break this down:
- ⁷√7 is the magnitude (or modulus) of each solution.
- e^(i * (2πk)/6) represents the complex phase, the angle in the complex plane.
- 'k' is an integer index that cycles through the six solutions.
By substituting the values of k (0 to 5), we obtain the six distinct roots:
k = 0: x₀ = ⁷√7 * e^(i*0) = ⁷√7 (our principal real root)
k = 1: x₁ = ⁷√7 * e^(iπ/3) = ⁷√7 * (cos(π/3) + i sin(π/3))
k = 2: x₂ = ⁷√7 * e^(i2π/3) = ⁷√7 * (cos(2π/3) + i sin(2π/3))
k = 3: x₃ = ⁷√7 * e^(iπ) = -⁷√7 (another real root – the negative counterpart)
k = 4: x₄ = ⁷√7 * e^(i4π/3) = ⁷√7 * (cos(4π/3) + i sin(4π/3))
k = 5: x₅ = ⁷√7 * e^(i5π/3) = ⁷√7 * (cos(5π/3) + i sin(5π/3))
These are our six solutions. Notice that we have two real solutions (x₀ and x₃) and four complex solutions (x₁, x₂, x₄, and x₅). The complex solutions come in conjugate pairs, as is typical with polynomial equations with real coefficients.
Visualizing the Solutions in the Complex Plane
Plotting these solutions on the complex plane helps visualize their distribution. They form a regular hexagon centered at the origin, with each vertex representing one of the six solutions. The distance of each vertex from the origin is ⁷√7.
Practical Applications and Broader Significance
Solving higher-order equations like x⁶ = 7 is not just an academic exercise. These types of equations arise in various applications including:
- Engineering: Analyzing oscillatory systems, signal processing, and control systems frequently involve solving higher-order polynomial equations.
- Physics: Quantum mechanics, wave mechanics, and other areas of physics often require finding the roots of complex polynomial equations to describe physical phenomena.
- Computer Graphics: Calculating transformations and rotations in computer graphics utilizes complex numbers and often involves higher-order polynomial solutions.
- Cryptography: Certain cryptographic algorithms rely on the properties of polynomials and their roots for security.
Numerical Methods for Approximating Solutions
For higher-order equations that don't have easily identifiable solutions (like some higher-degree polynomials), numerical methods provide approximate solutions. These include:
- Newton-Raphson method: An iterative method that refines an initial guess to converge towards a solution.
- Bisection method: A bracketing method that repeatedly divides an interval containing a root until the desired accuracy is achieved.
These methods are crucial when analytical solutions are impossible or impractical to find.
Conclusion: A Comprehensive Look at Polynomial Roots
The seemingly simple equation x⁶ = 7 opens a door to a rich understanding of complex numbers, roots of unity, and the fundamental theorem of algebra. By exploring both real and complex solutions, and understanding the broader context of polynomial equations and their applications, we gain a deeper appreciation for the power and elegance of mathematics. Whether tackling analytical solutions or relying on numerical approximation techniques, understanding the methods of solving higher-order equations is crucial across various disciplines. This exploration emphasizes the interconnectedness of mathematical concepts and their vital role in solving real-world problems.
Latest Posts
Latest Posts
-
Is 19 A Composite Or Prime Number
May 12, 2025
-
Which Of The Following Reactions Is Not A Redox Reaction
May 12, 2025
-
What Are The Final Products Of Meiosis
May 12, 2025
-
What Do You Call North South East And West
May 12, 2025
-
Write Five And Twenty Two Thousandths As A Decimal
May 12, 2025
Related Post
Thank you for visiting our website which covers about If X 6 7 Then X Is Equal To . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.