How To Find The Sum Of Interior Angles
Juapaving
Apr 06, 2025 · 6 min read
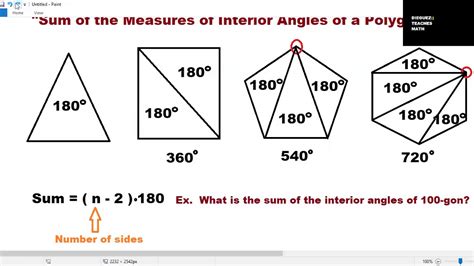
Table of Contents
How to Find the Sum of Interior Angles: A Comprehensive Guide
Understanding how to find the sum of interior angles is a fundamental concept in geometry, crucial for solving various problems related to polygons. This comprehensive guide will explore different methods for calculating the sum of interior angles, catering to various levels of mathematical understanding, from beginners to more advanced learners. We'll delve into the formulas, provide practical examples, and explore the underlying principles behind these calculations.
Understanding Polygons
Before we delve into the methods for calculating the sum of interior angles, let's establish a firm understanding of what polygons are. A polygon is a closed two-dimensional geometric figure composed of straight line segments. These segments are called sides, and the points where two sides meet are called vertices. Polygons are classified based on the number of sides they possess:
- Triangle: 3 sides
- Quadrilateral: 4 sides
- Pentagon: 5 sides
- Hexagon: 6 sides
- Heptagon: 7 sides
- Octagon: 8 sides
- Nonagon: 9 sides
- Decagon: 10 sides
- And so on...
The number of sides directly relates to the number of interior angles a polygon has. For example, a triangle has three interior angles, a quadrilateral has four, and so on. The sum of these interior angles is what we aim to calculate.
Method 1: Using the Formula for the Sum of Interior Angles
The most straightforward and efficient method for finding the sum of interior angles of any polygon is using a specific formula. This formula relies on the number of sides (n) of the polygon:
Sum of Interior Angles = (n - 2) × 180°
Where 'n' represents the number of sides of the polygon.
This formula is derived from the fact that any polygon can be divided into triangles by drawing diagonals from one vertex to all other non-adjacent vertices. The number of triangles formed is always two less than the number of sides. Since the sum of angles in a triangle is always 180°, multiplying this by the number of triangles gives the total sum of interior angles.
Examples:
1. Finding the sum of interior angles of a pentagon:
A pentagon has 5 sides (n = 5). Using the formula:
Sum of Interior Angles = (5 - 2) × 180° = 3 × 180° = 540°
2. Finding the sum of interior angles of a decagon:
A decagon has 10 sides (n = 10). Using the formula:
Sum of Interior Angles = (10 - 2) × 180° = 8 × 180° = 1440°
3. Finding the sum of interior angles of a hexagon:
A hexagon has 6 sides (n=6). Using the formula:
Sum of Interior Angles = (6-2) x 180° = 4 x 180° = 720°
Method 2: Dividing the Polygon into Triangles
This method provides a visual and intuitive understanding of why the formula works. It involves dividing the polygon into triangles by drawing diagonals from a single vertex to all other non-adjacent vertices. The number of triangles formed will always be two less than the number of sides of the polygon.
Steps:
- Choose a vertex: Select any vertex of the polygon.
- Draw diagonals: Draw diagonals from the chosen vertex to all other non-adjacent vertices. Avoid drawing diagonals that overlap.
- Count the triangles: Count the number of triangles formed.
- Calculate the sum: Multiply the number of triangles by 180° (the sum of angles in a triangle).
This method is particularly useful for visualizing the concept and for polygons with a relatively small number of sides. However, for polygons with many sides, the formula remains the most efficient approach.
Example: Finding the sum of interior angles of a quadrilateral using this method.
- Choose a vertex: Select any of the four vertices.
- Draw diagonals: Draw one diagonal, dividing the quadrilateral into two triangles.
- Count the triangles: There are two triangles.
- Calculate the sum: 2 × 180° = 360°
This confirms the result obtained using the formula (n-2) x 180° where n=4.
Method 3: Understanding Regular Polygons
A regular polygon is a polygon where all sides are of equal length, and all interior angles are of equal measure. Finding the measure of a single interior angle in a regular polygon is a straightforward extension of the sum of interior angles formula.
To find the measure of a single interior angle in a regular polygon:
- Calculate the sum of interior angles: Use the formula (n - 2) × 180°.
- Divide by the number of angles: Divide the sum by the number of sides (n), which is also the number of angles.
Formula for a single interior angle of a regular polygon:
Single Interior Angle = [(n - 2) × 180°] / n
Example: Finding the measure of a single interior angle in a regular hexagon:
- Calculate the sum of interior angles: (6 - 2) × 180° = 720°
- Divide by the number of angles: 720° / 6 = 120°
Therefore, each interior angle in a regular hexagon measures 120°.
Advanced Concepts and Applications
The concepts discussed above form the foundation for understanding and solving various problems in geometry and related fields. Here are some advanced applications:
- Tessellations: Understanding the sum of interior angles is crucial in determining which polygons can tessellate (tile a plane without gaps or overlaps). Only polygons whose interior angles add up to a multiple of 360° can tessellate.
- Finding exterior angles: The sum of exterior angles (one at each vertex) of any polygon is always 360°. This is irrespective of the number of sides. This property is useful in solving problems involving exterior angles and their relationship with interior angles.
- Solving geometric proofs: The sum of interior angles formula is frequently used in geometric proofs to demonstrate relationships between angles and sides of polygons.
- Three-dimensional geometry: The principles of calculating interior angles extend to three-dimensional shapes, such as polyhedra. Understanding the sum of interior angles of the faces of a polyhedron is important in various three-dimensional geometric calculations.
Troubleshooting Common Mistakes
When calculating the sum of interior angles, several common mistakes can occur:
- Incorrectly applying the formula: Ensure you are subtracting 2 from the number of sides before multiplying by 180°.
- Confusing interior and exterior angles: Remember the sum of exterior angles is always 360°, while the sum of interior angles depends on the number of sides.
- Not considering regular polygons: The formula for a single interior angle only applies to regular polygons where all angles are equal.
Always double-check your calculations and carefully consider the type of polygon you are working with to avoid these common pitfalls.
Conclusion
Finding the sum of interior angles of a polygon is a fundamental skill in geometry with diverse applications. By understanding the formula, the method of dividing into triangles, and the properties of regular polygons, you can confidently solve a wide range of geometric problems. Remember to practice applying these methods to solidify your understanding and build your problem-solving skills. This knowledge forms a crucial base for more advanced geometric concepts and their applications in various fields. Continue exploring these mathematical principles to expand your understanding and mastery of geometry.
Latest Posts
Latest Posts
-
Which Of The Following Is A Nonrenewable Source Of Energy
Apr 08, 2025
-
Difference Between Sn1 And Sn2 Reactions
Apr 08, 2025
-
What Is The Mode Of Nutrition For Plants
Apr 08, 2025
-
Is Density And Specific Gravity The Same
Apr 08, 2025
-
Which Of The Following Cells Are Found In Cartilage
Apr 08, 2025
Related Post
Thank you for visiting our website which covers about How To Find The Sum Of Interior Angles . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.