How To Find The Orthocenter Of An Obtuse Triangle
Juapaving
Mar 30, 2025 · 6 min read
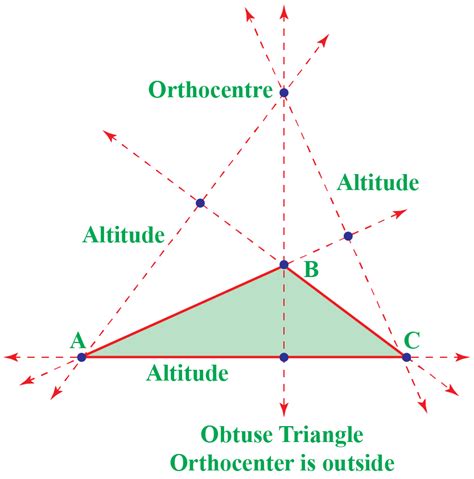
Table of Contents
How to Find the Orthocenter of an Obtuse Triangle
The orthocenter, a fascinating point within a triangle, holds a unique position as the intersection of its altitudes. Understanding how to locate this point is crucial for various geometric applications and problem-solving. While straightforward for acute triangles, finding the orthocenter of an obtuse triangle requires a slightly different approach due to the exterior intersection of one or more altitudes. This comprehensive guide will equip you with the knowledge and techniques to pinpoint the orthocenter of any obtuse triangle, regardless of its specific dimensions or angles.
Understanding the Orthocenter and Obtuse Triangles
Before diving into the methods, let's establish a solid foundation.
What is an Orthocenter?
The orthocenter of a triangle is the point where all three altitudes of the triangle intersect. An altitude is a line segment drawn from a vertex of the triangle perpendicular to the opposite side (or its extension). This intersection point is a significant feature in the study of triangles and possesses several intriguing geometric properties.
What is an Obtuse Triangle?
An obtuse triangle is a triangle with one interior angle greater than 90 degrees (an obtuse angle). This characteristic distinguishes it from acute triangles (all angles less than 90 degrees) and right triangles (one angle exactly 90 degrees). The presence of an obtuse angle significantly impacts the location of the orthocenter in an obtuse triangle. Unlike acute triangles where the orthocenter lies inside the triangle, the orthocenter of an obtuse triangle lies outside the triangle.
Methods for Finding the Orthocenter of an Obtuse Triangle
Several methods can be employed to determine the orthocenter of an obtuse triangle. We will explore three primary approaches:
Method 1: Using Graph Paper and Ruler
This is a visual and hands-on method, ideal for understanding the concept and performing calculations for specific triangles.
-
Draw the Triangle: Accurately draw the obtuse triangle on graph paper, ensuring the sides are measured and angles are as close to the correct values as possible. Label the vertices A, B, and C.
-
Construct the Altitudes: For each vertex, draw a line perpendicular to the opposite side. This requires careful use of a ruler and protractor (or a set square for accuracy). Remember, for the obtuse angle, the altitude will extend outside the triangle.
-
Locate the Intersection: The point where these three altitudes intersect is the orthocenter. Mark this point clearly and label it H.
Advantages: This method provides a clear visual representation and enhances understanding.
Disadvantages: Subject to inaccuracies due to manual drawing and measurement, it's not suitable for high-precision calculations or abstract problems. Also, it becomes cumbersome for triangles with complex dimensions.
Method 2: Using Coordinate Geometry
This is a powerful algebraic method suitable for precise calculations and applicable to triangles defined by coordinates.
-
Assign Coordinates: Assign Cartesian coordinates (x, y) to each vertex of the triangle. For example, let A = (x₁, y₁), B = (x₂, y₂), and C = (x₃, y₃).
-
Determine the Slopes: Calculate the slopes (m) of the sides of the triangle using the formula: m = (y₂ - y₁) / (x₂ - x₁) for side AB, and similarly for BC and AC.
-
Find the Slopes of the Altitudes: The slope of an altitude is the negative reciprocal of the slope of the side it's perpendicular to. For example, the altitude from A to BC will have a slope of -1/m(BC).
-
Find the Equations of the Altitudes: Using the point-slope form of a linear equation (y - y₁ = m(x - x₁)), write the equations of at least two altitudes. For instance, using the altitude from A and the coordinates of A, you can generate the equation.
-
Solve the System of Equations: Solve the system of equations formed by any two altitudes simultaneously. The solution (x, y) represents the coordinates of the orthocenter.
Example:
Let's say A = (1, 2), B = (4, 1), and C = (2, 5).
- Slope of BC: m(BC) = (5 - 1) / (2 - 4) = -2
- Slope of altitude from A: -1/m(BC) = 1/2
- Equation of altitude from A: y - 2 = (1/2)(x - 1) => y = (1/2)x + 3/2
Repeat this process for another altitude (e.g., from B or C) and solve the resulting system of two linear equations to find the orthocenter's coordinates.
Advantages: Provides precise coordinates, suitable for complex triangles, and easily adaptable to computer programming.
Disadvantages: Requires a strong understanding of algebra and coordinate geometry. Can become computationally intensive for very large or complex values.
Method 3: Using Trigonometry
This method utilizes trigonometric functions and is particularly useful when dealing with triangles defined by angles and side lengths.
-
Identify the Obtuse Angle: Determine which angle in the triangle is obtuse (greater than 90 degrees). Let's call this angle C.
-
Use the Law of Sines: The law of sines states that a/sin(A) = b/sin(B) = c/sin(C), where a, b, and c are the side lengths opposite angles A, B, and C respectively.
-
Apply Trigonometric Identities: Employ trigonometric identities and the properties of altitudes to derive expressions for the coordinates of the orthocenter in terms of side lengths and angles. This often involves using the sine and cosine rules, and potentially solving multiple equations simultaneously.
-
Solve for the Orthocenter: This process is algebraically more involved and requires a good grasp of trigonometric identities. The resulting coordinates represent the orthocenter.
Advantages: Suitable when the triangle is defined by angles and side lengths.
Disadvantages: Highly complex algebraically, not ideal for beginners, and demands a solid understanding of trigonometry.
Choosing the Right Method
The optimal method depends on the context and the available information:
- Visual understanding and simple triangles: Graph paper and ruler.
- Precise coordinates and algebraic approach: Coordinate geometry.
- Triangles defined by angles and sides and advanced trigonometric knowledge: Trigonometry.
Practical Applications and Further Exploration
Understanding the orthocenter extends beyond theoretical geometry. It has applications in:
- Computer graphics: Used in algorithms for generating and manipulating geometric shapes.
- Engineering and design: Useful in structural analysis and design of frameworks.
- Physics: Appears in various physical phenomena related to vector analysis and force equilibrium.
By mastering the techniques outlined above, you'll be well-equipped to locate the orthocenter of any obtuse triangle, unlocking deeper understanding within the world of geometry. Remember to choose the method best suited to your needs and available information. Further exploration into geometric properties linked to the orthocenter, such as its relationship to the circumcenter and centroid, will further enhance your mathematical understanding and problem-solving skills. The orthocenter, while seemingly a simple point, is a gateway to a rich tapestry of geometric relationships and applications.
Latest Posts
Latest Posts
-
Least Common Multiple Of 28 And 32
Apr 01, 2025
-
What Is The Square Root Of 676
Apr 01, 2025
-
How Many Kings Are In A Deck Of 52
Apr 01, 2025
-
What Is The Capacity To Do Work Called
Apr 01, 2025
-
Why Should You Always Transcribe Files On Your Own
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about How To Find The Orthocenter Of An Obtuse Triangle . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
