How To Find The Equation Of A Horizontal Line
Juapaving
Apr 07, 2025 · 5 min read
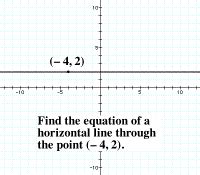
Table of Contents
How to Find the Equation of a Horizontal Line: A Comprehensive Guide
Finding the equation of a horizontal line might seem trivial at first glance, but understanding its underlying principles is crucial for grasping more complex mathematical concepts. This comprehensive guide will delve into the intricacies of horizontal lines, explaining not only how to find their equations but also the reasons behind the methods and their practical applications.
Understanding the Nature of Horizontal Lines
Before diving into the equation itself, let's solidify our understanding of what constitutes a horizontal line. A horizontal line is a straight line that runs parallel to the x-axis. This means it has zero slope or zero gradient. Every point on a horizontal line shares the same y-coordinate, regardless of its x-coordinate. This characteristic is the key to understanding its equation.
Visualizing a Horizontal Line
Imagine a perfectly flat line stretching infinitely to the left and right. This is the visual representation of a horizontal line. No matter how far you move along this line, you will never change your vertical position (your y-coordinate). This unchanging y-coordinate is what defines the line.
Contrasting with Vertical and Slanted Lines
To fully appreciate the unique properties of horizontal lines, it's beneficial to compare them to vertical and slanted lines.
-
Vertical Lines: These lines run parallel to the y-axis and have an undefined slope. Their equation is of the form x = c, where 'c' is a constant representing the x-intercept.
-
Slanted Lines: These lines have a defined, non-zero slope. Their equation is typically represented in slope-intercept form (y = mx + b), where 'm' is the slope and 'b' is the y-intercept.
Deriving the Equation of a Horizontal Line
The defining characteristic of a horizontal line—its constant y-coordinate—directly leads to its equation. Since the y-coordinate remains unchanged regardless of the x-coordinate, the equation is simply:
y = k
where 'k' is a constant representing the y-coordinate of every point on the line. This 'k' value is also the y-intercept of the horizontal line.
Step-by-Step Process
Let's break down the process of finding the equation of a horizontal line into simple steps:
-
Identify a point on the line: You only need one point (x, y) that lies on the horizontal line.
-
Extract the y-coordinate: The y-coordinate of this point is the crucial piece of information.
-
Substitute into the equation: Substitute the y-coordinate into the equation y = k, where k represents the y-coordinate.
-
Write the final equation: The resulting equation, y = k, is the equation of the horizontal line.
Example 1: Finding the Equation Given a Point
Let's say a point (3, 5) lies on a horizontal line.
-
Point: (3, 5)
-
Y-coordinate: 5
-
Substitution: y = 5
-
Equation: The equation of the horizontal line is y = 5. This means every point on the line has a y-coordinate of 5, regardless of its x-coordinate. Points like (0, 5), (-2, 5), and (100, 5) all lie on this line.
Example 2: Finding the Equation Given Two Points
Even if you're given two points on the horizontal line, the process remains straightforward. Remember, both points will have the same y-coordinate.
Let's consider the points (-1, 2) and (4, 2).
-
Points: (-1, 2) and (4, 2)
-
Y-coordinate: Both points have a y-coordinate of 2.
-
Substitution: y = 2
-
Equation: The equation of the horizontal line is y = 2.
Practical Applications of Horizontal Lines
Horizontal lines are not just abstract mathematical concepts; they have numerous practical applications across various fields.
1. Graphing and Data Representation:
Horizontal lines are frequently used in graphs and charts to represent constant values or benchmarks. For example, in a line graph showing temperature over time, a horizontal line might represent a specific temperature threshold. In bar charts, a horizontal line could depict an average value.
2. Geometry and Coordinate Systems:
Understanding horizontal lines is fundamental to many geometric concepts. For instance, finding the distance between a point and a horizontal line involves simple calculations based on the y-coordinate.
3. Calculus and Derivatives:
In calculus, the derivative of a horizontal line is always zero, reflecting its constant slope. This is a cornerstone concept in understanding rates of change and optimization problems.
4. Computer Graphics and Game Development:
In computer graphics and game development, horizontal lines are essential for creating various visual elements, from simple borders and UI elements to more complex game environments. They're building blocks for more advanced shapes and textures.
5. Engineering and Physics:
Horizontal lines are used extensively in various engineering and physics applications. For example, they might represent a level surface in surveying or a constant force in a physics problem.
Common Mistakes to Avoid
While finding the equation of a horizontal line is relatively simple, there are a few common mistakes beginners might make:
-
Confusing with Vertical Lines: Remember, the equation for a vertical line is x = c, not y = c. Understanding the difference between horizontal and vertical lines is paramount.
-
Incorrectly Identifying the Constant: Always make sure to correctly identify the constant y-coordinate. A simple error in reading the coordinates can lead to the wrong equation.
-
Overcomplicating the Problem: The equation of a horizontal line is straightforward; don't try to apply more complex methods unnecessarily.
Advanced Considerations
While the basic equation y = k suffices for most applications, more advanced situations might require a slightly different approach:
-
Parametric Equations: A horizontal line can also be represented using parametric equations. For example, x = t and y = k, where 't' is a parameter.
-
Vector Equations: In vector form, a horizontal line can be expressed as r = a + λb, where a is a position vector of a point on the line, b is a direction vector (in this case, parallel to the x-axis), and λ is a scalar parameter.
Conclusion
Finding the equation of a horizontal line is a fundamental concept in mathematics with broad applications. By understanding its underlying principles and avoiding common mistakes, you can confidently tackle various mathematical and real-world problems involving horizontal lines. Remember, the key is to identify the constant y-coordinate and use the simple equation y = k to represent the line. Mastering this seemingly simple concept lays a strong foundation for understanding more advanced mathematical topics.
Latest Posts
Latest Posts
-
How Many Feet Is 22 Inches
Apr 08, 2025
-
Things That Start With A Y
Apr 08, 2025
-
Energy Saved Is Energy Produced Assess The Statement
Apr 08, 2025
-
How Many Acres Is 1 Mile
Apr 08, 2025
-
What Is The Sqaure Root Of 36
Apr 08, 2025
Related Post
Thank you for visiting our website which covers about How To Find The Equation Of A Horizontal Line . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.