How Much Is 20 Of 1000
Juapaving
May 10, 2025 · 5 min read
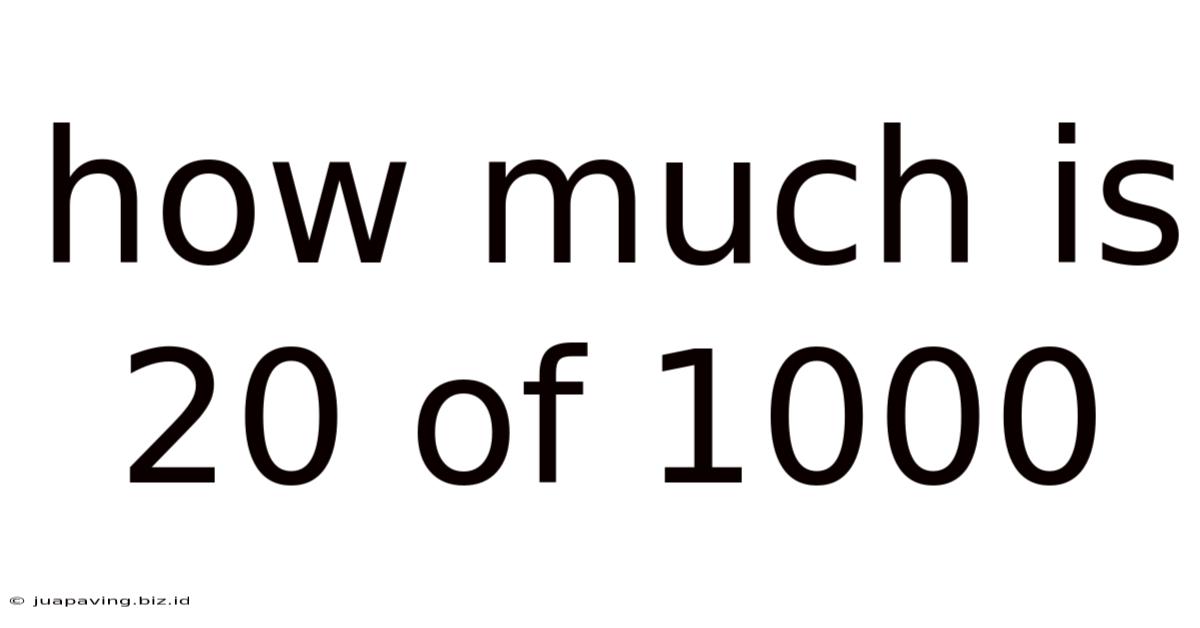
Table of Contents
How Much is 20% of 1000? A Deep Dive into Percentages and Their Applications
Calculating percentages is a fundamental skill with widespread applications in various aspects of life, from everyday budgeting and shopping to complex financial analyses and scientific research. Understanding how to determine a percentage of a given number is crucial for informed decision-making in both personal and professional contexts. This article will comprehensively explore how to calculate 20% of 1000, providing multiple methods, explaining the underlying concepts, and illustrating the practical applications of percentage calculations.
Understanding Percentages
A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "percent," which means "out of 100" or "per hundred." For example, 20% means 20 out of 100, which can be written as the fraction 20/100 or the decimal 0.20.
Method 1: Using the Decimal Method
This is arguably the most straightforward method for calculating percentages. It involves converting the percentage to a decimal and then multiplying it by the number.
Steps:
- Convert the percentage to a decimal: Divide the percentage by 100. In this case, 20% becomes 20/100 = 0.20.
- Multiply the decimal by the number: Multiply 0.20 by 1000. 0.20 * 1000 = 200
Therefore, 20% of 1000 is 200.
This method is efficient and easily applicable to various percentage calculations using a calculator or even mental arithmetic for simpler problems.
Method 2: Using the Fraction Method
This method leverages the fractional representation of percentages.
Steps:
- Express the percentage as a fraction: 20% can be written as 20/100.
- Simplify the fraction (if possible): 20/100 simplifies to 1/5.
- Multiply the fraction by the number: Multiply 1/5 by 1000. (1/5) * 1000 = 200
Therefore, 20% of 1000 is 200.
While this method might seem more complex at first glance, it provides a deeper understanding of the underlying mathematical principles and can be particularly useful when dealing with percentages that have easily simplified fractions.
Method 3: Using Proportions
This method involves setting up a proportion to solve for the unknown value.
Steps:
- Set up a proportion: We can set up a proportion as follows:
x/1000 = 20/100where 'x' represents 20% of 1000. - Cross-multiply: Multiply the numerator of one fraction by the denominator of the other, and vice-versa. This gives us:
100x = 20000. - Solve for x: Divide both sides of the equation by 100:
x = 20000/100 = 200
Therefore, 20% of 1000 is 200.
This method is particularly helpful in understanding the relationship between percentages and proportions and can be applied to a wide range of problems involving percentage calculations.
Real-World Applications of Percentage Calculations
The ability to calculate percentages accurately is essential in many real-world scenarios. Here are some examples:
- Finance: Calculating interest on loans, savings accounts, and investments. Understanding the interest rate (percentage) is crucial for making informed financial decisions. For instance, calculating the interest earned on a $1000 investment with a 20% annual interest rate.
- Sales and Discounts: Determining the discount amount on sale items. If a $1000 item is discounted by 20%, you'd save $200.
- Taxes: Computing sales tax, income tax, and other taxes based on percentages. Knowing your tax bracket (percentage) is crucial for budgeting.
- Statistics and Data Analysis: Calculating percentages in surveys, polls, and research to interpret data effectively.
- Science and Engineering: Percentage calculations are used extensively in fields like chemistry and physics to represent concentrations, efficiencies, and error margins.
- Everyday Life: Calculating tips in restaurants, figuring out sale prices, and determining the percentage of a project completed are everyday uses of percentage calculations.
Beyond the Basics: More Complex Percentage Problems
While the calculation of 20% of 1000 is relatively straightforward, the principles can be extended to more complex scenarios. Consider these examples:
- Calculating the percentage increase or decrease: This involves determining the percentage change between two values. For example, if a stock price increases from $1000 to $1200, the percentage increase is calculated as:
[(1200-1000)/1000] * 100% = 20%. - Finding the original amount given a percentage and the resulting amount: If 20% of a number is 200, to find the original number, you would use the inverse operation:
200 / 0.20 = 1000. - Compound Interest Calculations: These involve calculating interest on both the principal amount and accumulated interest over a period. Compound interest calculations are more complex but build upon the foundation of basic percentage calculations.
Mastering Percentage Calculations: Tips and Tricks
Here are some tips to improve your accuracy and efficiency in calculating percentages:
- Practice regularly: Consistent practice is key to mastering any skill, including percentage calculations.
- Use a calculator: Calculators can significantly improve accuracy and speed, especially for complex calculations.
- Understand the concepts: A thorough understanding of the underlying concepts will make problem-solving easier.
- Break down complex problems: Divide complex problems into smaller, manageable steps.
- Check your work: Always double-check your answers to ensure accuracy.
Conclusion
Calculating 20% of 1000, resulting in 200, is a fundamental percentage calculation with broad applications. This article has provided multiple methods for solving this problem, explained the underlying concepts of percentages, and illustrated their practical use in various contexts. Mastering percentage calculations is a valuable skill that enhances decision-making across personal and professional life. By understanding the different approaches and practicing regularly, you can confidently tackle more complex percentage problems and apply this knowledge effectively in various real-world scenarios. Remember, the ability to quickly and accurately calculate percentages empowers you to navigate the numerical world with greater ease and understanding.
Latest Posts
Latest Posts
-
23 11 Na Protons Neutrons Electrons
May 11, 2025
-
What Is The Base Of A Parallelogram
May 11, 2025
-
How Many Neutrons Does C14 Have
May 11, 2025
-
Words That Have X And W
May 11, 2025
-
What Temperature Does Water Freeze In Kelvin
May 11, 2025
Related Post
Thank you for visiting our website which covers about How Much Is 20 Of 1000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.