How Many Sides In A Rectangle
Juapaving
Mar 24, 2025 · 5 min read
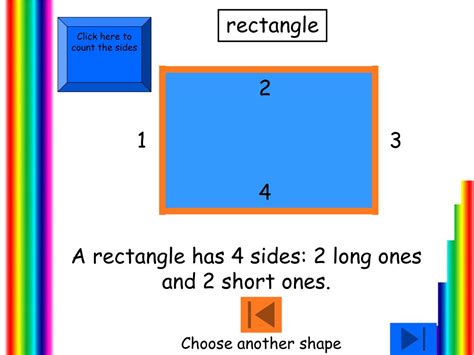
Table of Contents
- How Many Sides In A Rectangle
- Table of Contents
- How Many Sides Does a Rectangle Have? A Deep Dive into Geometry
- Defining a Rectangle: More Than Just Four Sides
- Distinguishing Rectangles from Other Quadrilaterals
- The Significance of the Four Sides: Applications and Real-World Examples
- Architecture and Construction:
- Everyday Objects:
- Mathematics and Geometry:
- Beyond the Basics: Exploring Advanced Concepts
- Diagonal Properties:
- Area and Perimeter: Optimization Problems
- Transformations of Rectangles:
- Conclusion: The Importance of Understanding Rectangles
- Latest Posts
- Latest Posts
- Related Post
How Many Sides Does a Rectangle Have? A Deep Dive into Geometry
The seemingly simple question, "How many sides does a rectangle have?" opens a door to a fascinating exploration of geometry, its properties, and its applications in the real world. While the answer might appear obvious to many – four – delving deeper reveals a rich understanding of shapes, their characteristics, and the mathematical principles that govern them. This article aims to provide a comprehensive answer, exploring the definition of a rectangle, its properties, related shapes, and real-world examples, all while employing strong SEO principles for optimal online visibility.
Defining a Rectangle: More Than Just Four Sides
A rectangle, at its most basic, is a quadrilateral, meaning a polygon with four sides. However, it's not just any four-sided shape; it possesses specific properties that distinguish it. These crucial characteristics are:
-
Four right angles (90 degrees): Each interior angle of a rectangle is a perfect right angle. This is a defining characteristic, differentiating it from other quadrilaterals like parallelograms or trapezoids.
-
Opposite sides are equal and parallel: The sides opposite each other in a rectangle have equal lengths and are parallel. This parallelism ensures the stability and symmetry of the shape.
-
Two pairs of parallel sides: This property is a direct consequence of the equal and parallel opposite sides.
These defining features ensure that a rectangle maintains its specific shape and properties, making it distinct from other four-sided polygons. Understanding these properties is crucial for solving geometrical problems and for applications in various fields.
Distinguishing Rectangles from Other Quadrilaterals
It's important to understand how rectangles relate to other quadrilaterals. Consider these key distinctions:
-
Square: A square is a special type of rectangle where all four sides are equal in length. So, a square is a rectangle, but a rectangle isn't necessarily a square.
-
Parallelogram: A parallelogram has opposite sides that are parallel and equal, but its angles are not necessarily right angles. A rectangle is a special case of a parallelogram where all angles are 90 degrees.
-
Rhombus: A rhombus has all four sides equal in length, but its angles are not necessarily right angles.
-
Trapezoid (or Trapezium): A trapezoid has only one pair of parallel sides, unlike a rectangle which has two pairs.
The Significance of the Four Sides: Applications and Real-World Examples
The four sides of a rectangle are not merely a defining characteristic; they are fundamental to its functionality and widespread use in various contexts. Let's explore some examples:
Architecture and Construction:
The rectangular shape is ubiquitous in architecture and construction. Buildings, rooms, doors, windows – they're almost always rectangular. This is due to several reasons:
-
Stability: The right angles and parallel sides provide structural stability, making rectangular structures strong and reliable.
-
Efficiency: Rectangles allow for efficient use of space and materials. They lend themselves to easy calculations for area and perimeter, simplifying the design and construction process.
-
Aesthetics: Rectangles often create a sense of order, balance, and proportion, making them aesthetically pleasing in many designs.
Everyday Objects:
Countless everyday objects are rectangular:
-
Books: The familiar rectangular shape of books is designed for easy storage and handling.
-
Tables and Desks: Rectangular tables and desks offer ample workspace and are easily adaptable to different environments.
-
Screens (TV, Computer, Phone): Most screens, regardless of their aspect ratio, are fundamentally rectangular.
-
Packaging: Boxes, containers, and packages are frequently rectangular for efficient stacking and transportation.
-
Playing Cards: The standard playing card is a perfect example of a rectangle in a widely used game.
Mathematics and Geometry:
Rectangles are fundamental to understanding area and perimeter calculations. The formulas:
-
Area = length × width
-
Perimeter = 2(length + width)
are crucial tools in various mathematical and geometrical problems. These calculations are essential for tasks ranging from designing floor plans to calculating the amount of material needed for a project.
Beyond the Basics: Exploring Advanced Concepts
While the number of sides is a fundamental property, understanding the geometry of a rectangle goes far beyond simply counting sides. Here are some more advanced concepts:
Diagonal Properties:
The diagonals of a rectangle possess interesting properties:
-
Equal Lengths: Both diagonals have equal lengths.
-
Bisecting Each Other: The diagonals bisect each other, meaning they intersect at their midpoints.
Understanding these diagonal properties is crucial for solving geometrical problems and proving theorems related to rectangles.
Area and Perimeter: Optimization Problems
Many real-world problems involve optimizing the area or perimeter of a rectangle given certain constraints. This involves calculus and optimization techniques. For example, finding the dimensions of a rectangular garden with a fixed perimeter that maximizes its area is a classic optimization problem.
Transformations of Rectangles:
Rectangles can be subject to various geometric transformations:
-
Rotation: Rotating a rectangle changes its orientation but doesn't alter its fundamental properties.
-
Translation: Moving a rectangle without rotating or resizing it.
-
Reflection: Reflecting a rectangle across a line produces a mirror image.
-
Dilation: Enlarging or reducing the size of a rectangle proportionally.
Conclusion: The Importance of Understanding Rectangles
The question of how many sides a rectangle has, while seemingly trivial, opens up a vast and rich field of mathematical exploration. From its fundamental properties to its advanced applications in various fields, the rectangle showcases the beauty and power of geometry. Its ubiquitous presence in our everyday lives underscores its importance, making it a fundamental shape worthy of thorough understanding. The four sides, along with its right angles and parallel sides, define its unique characteristics and applications, making it a cornerstone of geometrical study and practical applications across countless fields. Therefore, understanding the rectangle and its properties isn’t just about knowing its sides; it's about grasping the foundational principles of geometry and its impact on the world around us.
Latest Posts
Latest Posts
-
When Ice Cream Melts A Chemical Change Occurs
Mar 30, 2025
-
How To Tell Time On A Watch Without Numbers
Mar 30, 2025
-
How Many Km Are In 230 M
Mar 30, 2025
-
Definition Of Word Form In Math
Mar 30, 2025
-
How Much Is 200 Fahrenheit In Celsius
Mar 30, 2025
Related Post
Thank you for visiting our website which covers about How Many Sides In A Rectangle . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
