How Many Sides Do Nonagon Have
Juapaving
Apr 02, 2025 · 4 min read
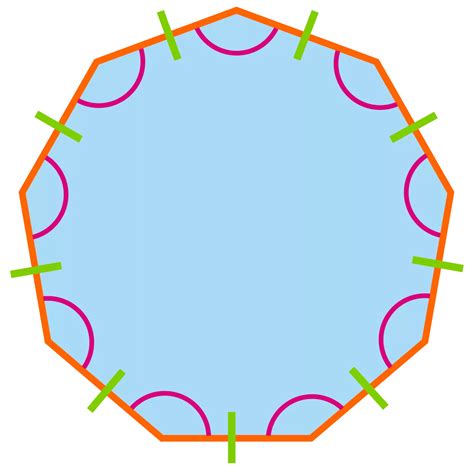
Table of Contents
- How Many Sides Do Nonagon Have
- Table of Contents
- How Many Sides Does a Nonagon Have? A Deep Dive into Nonagonal Geometry
- Understanding the Basics: Defining a Nonagon
- Regular vs. Irregular Nonagons
- Concave and Convex Nonagons
- Calculating the Area of a Nonagon
- Area of a Regular Nonagon
- Area of an Irregular Nonagon
- Nonagons in Real-World Applications
- Exploring Further: Beyond the Basics
- Conclusion: The Nine-Sided Wonder
- Latest Posts
- Latest Posts
- Related Post
How Many Sides Does a Nonagon Have? A Deep Dive into Nonagonal Geometry
The question, "How many sides does a nonagon have?" might seem trivial at first glance. The answer, of course, is nine. However, delving deeper into the properties of a nonagon reveals a fascinating world of geometry, encompassing various types, calculations, and applications. This comprehensive article will not only answer the fundamental question but also explore the intricacies of nonagons, their classifications, area calculations, and real-world applications.
Understanding the Basics: Defining a Nonagon
A nonagon is a polygon with nine sides and nine angles. The prefix "nona-" originates from the Latin word for nine. Like other polygons, nonagons can be classified based on their regularity and properties. Let's explore these classifications further.
Regular vs. Irregular Nonagons
A regular nonagon has all nine sides of equal length and all nine angles of equal measure. Each interior angle of a regular nonagon measures 140 degrees [(9-2) * 180 / 9 = 140]. This symmetrical nature simplifies many calculations related to its area and other geometric properties.
An irregular nonagon, on the other hand, has sides and angles of varying lengths and measures. There's a vast diversity within irregular nonagons, making calculations more complex and requiring specific measurements for accurate analysis. This variability allows for a wide array of shapes and forms.
Concave and Convex Nonagons
Beyond regularity, nonagons can also be classified as convex or concave. A convex nonagon has all its interior angles less than 180 degrees. A line segment connecting any two points within a convex nonagon lies entirely within the nonagon.
A concave nonagon has at least one interior angle greater than 180 degrees. This means at least one of its interior angles points inwards, creating a "dent" in the shape.
Calculating the Area of a Nonagon
The area calculation for a nonagon varies depending on whether it's regular or irregular.
Area of a Regular Nonagon
The area of a regular nonagon with side length 'a' can be calculated using the formula:
Area = (9/4) * a² * cot(π/9)
where 'cot' represents the cotangent function and 'π' (pi) is approximately 3.14159. This formula utilizes trigonometry to relate the side length to the area.
Alternatively, using the apothem (the distance from the center to the midpoint of a side), denoted as 'r':
Area = (9/2) * r² * tan(π/9)
This formula provides a convenient method if the apothem is known.
Area of an Irregular Nonagon
Calculating the area of an irregular nonagon is more complex. There's no single formula applicable to all irregular nonagons. The most common approach involves dividing the nonagon into smaller, simpler shapes such as triangles or trapezoids, calculating the area of each individual shape, and then summing up the individual areas to get the total area of the nonagon. Techniques like triangulation and coordinate geometry are often employed for this purpose.
Nonagons in Real-World Applications
While not as ubiquitous as triangles or squares, nonagons appear in various unexpected contexts:
-
Architecture and Design: While less common than other polygons, nonagons can be found in some architectural designs, particularly in creating unique floor plans or decorative elements. The unique shape offers a departure from standard designs.
-
Tessellations: Although regular nonagons cannot tessellate (tile a plane without gaps), certain combinations of nonagons with other polygons can create interesting and complex tessellations in art and design.
-
Engineering: Nonagonal shapes might appear in specialized engineering applications, particularly in creating components with unique geometric requirements. The nine-sided shape provides a specific set of properties that might be beneficial in certain mechanical designs.
-
Nature: While not as prevalent as other shapes found in nature, the nonagonal shape occasionally emerges in naturally occurring patterns, though this is less frequent than other polygonal shapes.
Exploring Further: Beyond the Basics
The study of nonagons extends beyond simple area calculations. More advanced topics include:
-
Nonagon constructions: Exploring different methods of constructing nonagons, both regular and irregular, using various geometric tools.
-
Inscribed and circumscribed circles: Investigating the relationships between nonagons and their inscribed and circumscribed circles, particularly in regular nonagons.
-
Symmetry groups of nonagons: Analyzing the symmetry properties of nonagons, particularly regular nonagons, and relating them to group theory concepts.
Conclusion: The Nine-Sided Wonder
The humble nonagon, with its nine sides, offers a rich landscape for exploration in the world of geometry. From the simplicity of its definition to the complexity of its area calculations for irregular forms, the nonagon provides a window into the fascinating world of polygons. Its presence, though less prominent than other polygons, can be found in unexpected corners of architecture, design, and engineering, showcasing the versatility of this nine-sided shape. Understanding the properties and characteristics of nonagons opens up a deeper appreciation for geometric principles and their application in the world around us. The next time you encounter a nine-sided figure, remember the intricate world of geometry hidden within this seemingly simple shape. This deep dive has hopefully provided a more comprehensive understanding, moving beyond the simple answer of "nine sides" to reveal the nuanced complexities of this unique polygon.
Latest Posts
Latest Posts
-
Describe Two Major Shortcomings Of Bohrs Model Of The Atom
Apr 04, 2025
-
How Many Feet Are In 64 Inches
Apr 04, 2025
-
Which Is A Renewable Resource Petroleum Wood Iron Coal
Apr 04, 2025
-
Which Of The Following Affects The Ocean Salinity
Apr 04, 2025
-
How Many 1000s In A Million
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about How Many Sides Do Nonagon Have . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
