How Many Lines Of Symmetry Does A Regular Triangle Have
Juapaving
May 11, 2025 · 5 min read
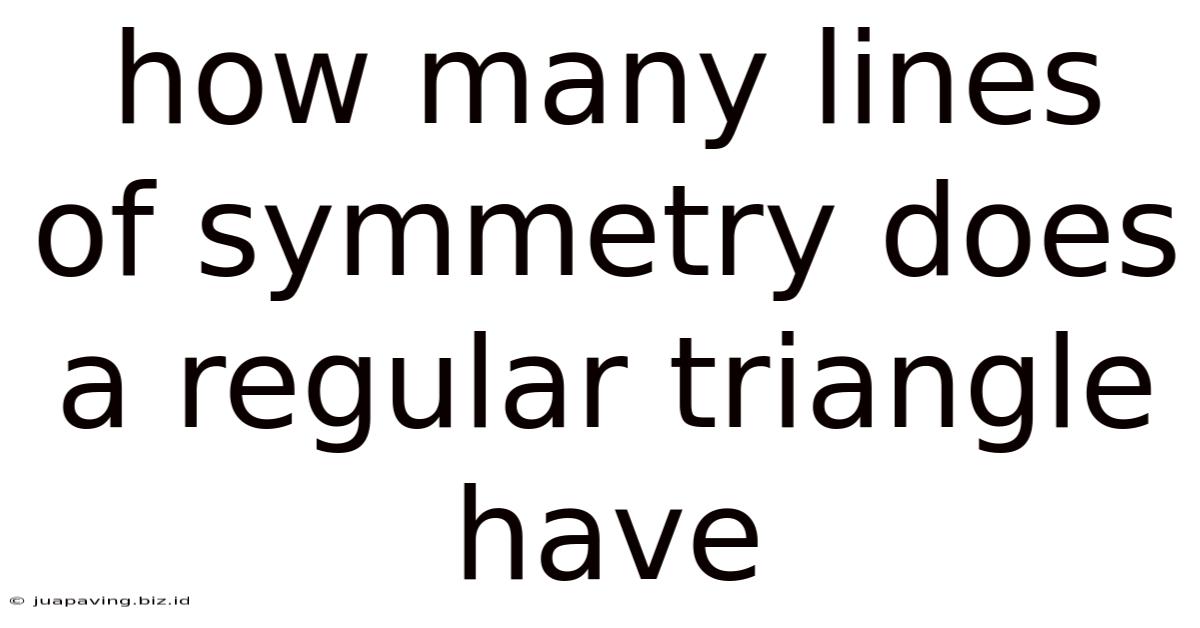
Table of Contents
How Many Lines of Symmetry Does a Regular Triangle Have? A Comprehensive Exploration
Symmetry, a fundamental concept in mathematics and geometry, plays a crucial role in understanding the properties of shapes. A line of symmetry, also known as a line of reflection, divides a shape into two identical halves that are mirror images of each other. This article delves into the fascinating world of symmetry, focusing specifically on the number of lines of symmetry possessed by a regular triangle, also known as an equilateral triangle. We'll explore the definition of symmetry, examine different types of triangles, and ultimately determine the answer to our central question.
Understanding Symmetry and Lines of Symmetry
Before diving into the specifics of triangles, let's establish a clear understanding of symmetry. Symmetry is a property of an object that remains unchanged under certain transformations, such as reflection, rotation, or translation. A shape exhibits reflectional symmetry if it can be folded along a line so that the two halves perfectly overlap. This line of folding is known as a line of symmetry, a axis of symmetry, or a reflectional axis.
Types of Symmetry
It's important to differentiate between various types of symmetry:
- Reflectional Symmetry (Line Symmetry): As discussed, this refers to a shape's ability to be folded along a line, resulting in identical halves.
- Rotational Symmetry: A shape possesses rotational symmetry if it can be rotated about a central point by a certain angle and still appear unchanged. The order of rotational symmetry indicates how many times the shape can be rotated before returning to its original orientation.
- Translational Symmetry: This type of symmetry applies to patterns that repeat themselves in a specific direction.
Exploring Triangles: A Deep Dive
Triangles, fundamental geometric shapes, are classified based on their side lengths and angles. Understanding these classifications is crucial for analyzing their symmetry.
Types of Triangles Based on Side Lengths:
- Equilateral Triangle: All three sides are of equal length.
- Isosceles Triangle: Two sides are of equal length.
- Scalene Triangle: All three sides are of different lengths.
Types of Triangles Based on Angles:
- Acute Triangle: All three angles are less than 90 degrees.
- Right Triangle: One angle is exactly 90 degrees.
- Obtuse Triangle: One angle is greater than 90 degrees.
Lines of Symmetry in Different Triangles
Let's analyze the number of lines of symmetry in each type of triangle:
1. Equilateral Triangle: The Symmetrical Champion
An equilateral triangle, with all three sides and angles equal (60 degrees each), boasts the highest degree of symmetry amongst triangles. It possesses three lines of symmetry. These lines are:
- One line connecting a vertex to the midpoint of the opposite side (an altitude and median). Folding the triangle along any of these lines creates two perfectly overlapping halves. Since there are three vertices, there are three such lines.
- These lines also bisect the angles. Each line of symmetry divides a 60-degree angle into two 30-degree angles.
This high degree of symmetry makes the equilateral triangle a visually pleasing and mathematically significant shape.
2. Isosceles Triangle: A Balanced Act
An isosceles triangle, with two equal sides, possesses one line of symmetry. This line:
- Connects the vertex formed by the two equal sides to the midpoint of the unequal side. This line is also an altitude, a median, and an angle bisector. Folding the triangle along this line results in two congruent halves.
Unlike the equilateral triangle, an isosceles triangle does not have multiple lines of symmetry. The unequal side prevents further symmetrical divisions.
3. Scalene Triangle: Asymmetry Reigns
A scalene triangle, possessing three unequal sides and three unequal angles, exhibits no lines of symmetry. There's no line that can divide it into two identical mirror images. The lack of symmetry distinguishes it from the other two types of triangles.
Proof of Three Lines of Symmetry in an Equilateral Triangle
Let's delve into a more formal proof of the three lines of symmetry in an equilateral triangle:
-
Consider an equilateral triangle ABC. All sides (AB, BC, CA) are equal in length, and all angles (∠A, ∠B, ∠C) are 60 degrees.
-
Draw a line from vertex A to the midpoint D of the opposite side BC. This line AD is both an altitude (perpendicular to BC) and a median (bisecting BC).
-
Fold the triangle along AD. The two halves, ΔABD and ΔACD, will perfectly overlap. This proves AD is a line of symmetry.
-
Repeat steps 2 and 3 for vertices B and C. Drawing lines from B to the midpoint of AC and from C to the midpoint of AB will similarly demonstrate that these are also lines of symmetry.
-
Therefore, an equilateral triangle has three lines of symmetry.
Practical Applications of Symmetry in Triangles
Understanding the symmetry of triangles is crucial in various fields:
-
Architecture and Design: Symmetrical shapes, including equilateral triangles, are aesthetically pleasing and structurally stable. Many architectural designs incorporate triangular elements to leverage their inherent strength and visual appeal.
-
Engineering: Understanding the symmetrical properties of triangles is essential in structural engineering for designing stable and efficient structures. Trusses, for instance, often utilize triangular elements due to their strength.
-
Art and Nature: Equilateral triangles appear frequently in art and nature, reflecting their inherent beauty and mathematical elegance. Many natural formations, like snowflakes, exhibit triangular patterns and elements of symmetry.
-
Computer Graphics and Animation: Computer graphics and animation heavily rely on symmetry concepts for creating realistic and efficient models. Symmetrical shapes are easier to model and animate, saving time and computational resources.
Beyond Triangles: Exploring Symmetry in Other Shapes
The concept of lines of symmetry extends beyond triangles to other shapes. For instance:
- Square: A square has four lines of symmetry: two diagonals and two lines connecting the midpoints of opposite sides.
- Rectangle: A rectangle has two lines of symmetry: lines connecting the midpoints of opposite sides.
- Circle: A circle has infinitely many lines of symmetry, with any diameter acting as a line of symmetry.
Conclusion: The Elegance of Symmetry
In conclusion, a regular triangle, or equilateral triangle, possesses three lines of symmetry. This inherent symmetry contributes to its mathematical elegance and widespread use in various fields. Understanding symmetry in shapes, including triangles, is fundamental to appreciating their geometric properties and applying them in diverse applications. From architectural marvels to natural formations, the principles of symmetry underpin the beauty and functionality we observe in the world around us. The exploration of symmetry is a journey into the heart of mathematical order and visual harmony.
Latest Posts
Latest Posts
-
Equal Opportunity Training Should Be Conducted At What Minimum Interval
Jun 01, 2025
-
Why Did Beatty Wanted To Die
Jun 01, 2025
-
All Of The Following Are Characteristics Of Professional Behavior Except
Jun 01, 2025
-
Creating Ld50 Graphs For Different Substances Worksheet Answer Key
Jun 01, 2025
-
Choose The Corresponding Pronoun They Nosotros Ustedes Usted Ellas
Jun 01, 2025
Related Post
Thank you for visiting our website which covers about How Many Lines Of Symmetry Does A Regular Triangle Have . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.