How Many Factors Does The Number 121 Have
Juapaving
Apr 06, 2025 · 4 min read
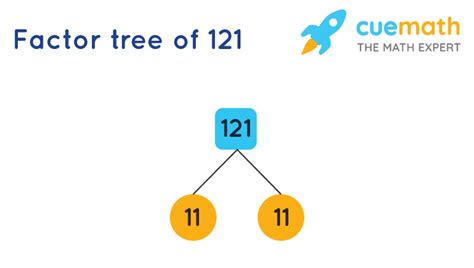
Table of Contents
How Many Factors Does the Number 121 Have? A Deep Dive into Factorization
Finding the number of factors for a given integer might seem like a simple mathematical task, but understanding the underlying principles reveals a fascinating connection between prime factorization and the structure of numbers. This article will explore how to determine the number of factors of 121, and more broadly, how to approach this problem for any integer. We'll delve into the concept of prime factorization, explore different methods for finding factors, and even touch upon the relationship between the number of factors and the properties of the number itself.
Understanding Prime Factorization
The cornerstone of finding the number of factors for any integer lies in its prime factorization. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself. Prime factorization is the process of expressing a number as a product of its prime factors. For instance, the prime factorization of 12 is 2 x 2 x 3 (or 2² x 3).
Prime Factorization of 121
Let's find the prime factorization of 121. We start by checking for the smallest prime numbers as divisors:
- Is 121 divisible by 2? No, because 121 is an odd number.
- Is 121 divisible by 3? No, because the sum of its digits (1 + 2 + 1 = 4) is not divisible by 3.
- Is 121 divisible by 5? No, because it doesn't end in 0 or 5.
- Is 121 divisible by 7? No, 121 divided by 7 leaves a remainder.
- Is 121 divisible by 11? Yes! 121 = 11 x 11.
Therefore, the prime factorization of 121 is 11². This means 121 is a perfect square, as it can be expressed as the square of a prime number.
Finding the Number of Factors
Once we have the prime factorization, calculating the number of factors becomes straightforward. Let's consider a general number, n, with the prime factorization:
n = p₁<sup>a₁</sup> * p₂<sup>a₂</sup> * p₃<sup>a₃</sup> ...
where pᵢ are distinct prime numbers and aᵢ are their respective exponents. The number of factors of n is given by the formula:
(a₁ + 1) * (a₂ + 1) * (a₃ + 1) ...
Applying the Formula to 121
Since the prime factorization of 121 is 11², we have:
- p₁ = 11
- a₁ = 2
Therefore, the number of factors of 121 is (2 + 1) = 3.
The Factors of 121
Let's list the factors of 121 to confirm our calculation:
- 1 (Every number has 1 as a factor)
- 11 (One of the prime factors)
- 121 (The number itself)
There are indeed three factors.
Extending the Concept: More Complex Examples
Let's analyze a more complex example to solidify our understanding. Consider the number 360:
-
Prime Factorization: 360 = 2³ x 3² x 5¹
-
Number of Factors: (3 + 1) x (2 + 1) x (1 + 1) = 4 x 3 x 2 = 24
Therefore, 360 has 24 factors.
Perfect Squares and the Number of Factors
Notice that perfect squares always have an odd number of factors. This is because the prime factorization of a perfect square will have even exponents for all its prime factors. Adding 1 to an even number always results in an odd number. Conversely, numbers that are not perfect squares will always have an even number of factors.
Applications and Further Exploration
Understanding the number of factors has applications in various areas of mathematics and computer science:
- Number Theory: Studying the distribution of factors helps us understand the properties of numbers and their relationships.
- Cryptography: Factorization is a crucial element in many cryptographic algorithms. Finding the factors of large numbers is computationally intensive, forming the basis of the security of many encryption methods.
- Combinatorics: Counting factors relates to the problem of counting divisors, a fundamental concept in combinatorics.
Conclusion: The Significance of Factorization
Determining the number of factors of a given integer, such as 121, is more than just a simple arithmetic exercise. It showcases the power of prime factorization and its ability to reveal hidden structural properties of numbers. The formula derived from prime factorization provides an efficient method for calculating the number of factors for any integer, regardless of its size or complexity. By understanding this process, we gain a deeper appreciation for the fundamental building blocks of numbers and their fascinating interconnectedness. This knowledge finds applications in various fields, highlighting the practical significance of this seemingly basic mathematical concept. Further exploration into the world of prime numbers and factorization will undoubtedly unveil even more intriguing aspects of number theory.
Latest Posts
Latest Posts
-
A Particle That Moves Around The Nucleus
Apr 09, 2025
-
Which Equation Represents A Nonlinear Function
Apr 09, 2025
-
Every Square Is A Rectangle True Or False
Apr 09, 2025
-
The Lymphatic System Differs From The Cardiovascular System In That
Apr 09, 2025
-
Words That Begin With A K
Apr 09, 2025
Related Post
Thank you for visiting our website which covers about How Many Factors Does The Number 121 Have . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.