How Many Even Integers Are There Between 200 And 700
Juapaving
Apr 14, 2025 · 4 min read
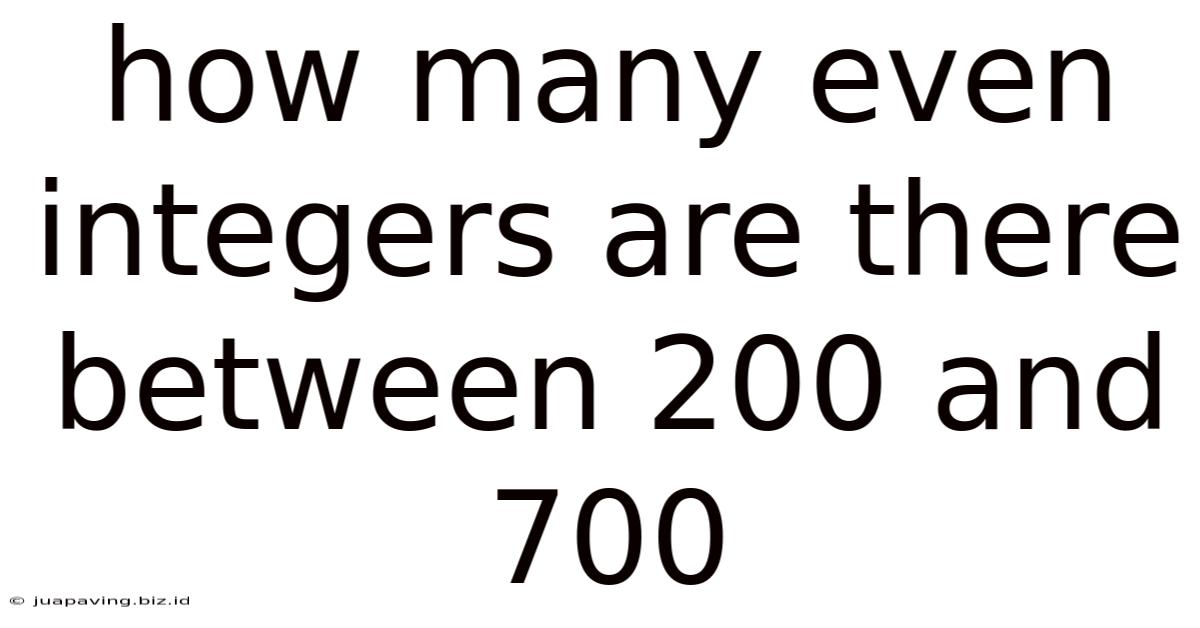
Table of Contents
How Many Even Integers Are There Between 200 and 700? A Comprehensive Guide
This seemingly simple question, "How many even integers are there between 200 and 700?", opens the door to a fascinating exploration of number theory and mathematical problem-solving. While a quick calculation might suffice for some, a deeper dive reveals opportunities to understand fundamental concepts and develop valuable analytical skills. This comprehensive guide will not only answer the question but will also explore various approaches to solving it, highlighting the underlying mathematical principles.
Understanding Even Integers
Before diving into the problem, let's clarify what we mean by "even integers." An even integer is any whole number that is perfectly divisible by 2, leaving no remainder. In other words, it's a number that can be expressed in the form 2n, where 'n' is any integer (positive, negative, or zero). Examples of even integers include 2, 4, 6, 8, 10, and so on.
Direct Counting Method: A Simple Approach
The most straightforward method to solve this problem is direct counting. We can list all even integers between 200 and 700 and then count them. While feasible for smaller ranges, this method becomes impractical for larger ranges. Let's try it for a smaller subset to illustrate the concept:
Let's find the number of even integers between 200 and 220. The even integers are 200, 202, 204, 206, 208, 210, 212, 214, 216, 218. There are 10 even integers.
However, manually counting all even integers between 200 and 700 would be tedious and error-prone. We need a more efficient method.
Arithmetic Sequence: A More Efficient Method
Even integers form an arithmetic sequence, a sequence where the difference between consecutive terms is constant. In this case, the common difference is 2. The first term (a₁) is 202, and the last term (aₙ) is 698. We can use the formula for the nth term of an arithmetic sequence to determine the number of terms:
aₙ = a₁ + (n-1)d
Where:
- aₙ is the nth term (698)
- a₁ is the first term (202)
- n is the number of terms (what we want to find)
- d is the common difference (2)
Let's plug in the values and solve for n:
698 = 202 + (n-1)2
Simplifying the equation:
496 = (n-1)2
248 = n-1
n = 249
Therefore, there are 249 even integers between 200 and 700.
Inclusive vs. Exclusive: Addressing Ambiguity
The phrasing "between 200 and 700" can sometimes be ambiguous. Does it include 200 and 700, or are they excluded? Our previous calculation assumed it's exclusive (meaning 200 and 700 are not included). If we were to include both 200 and 700, the first term would be 200 and the last term would be 700. Let's recalculate:
700 = 200 + (n-1)2 500 = (n-1)2 250 = n-1 n = 251
In this inclusive scenario, there would be 251 even integers. It’s crucial to clearly define the inclusion or exclusion of boundary values to avoid ambiguity in mathematical problems.
Visualizing with Number Lines
A number line can be a helpful tool for visualizing the problem. Imagine a number line extending from 200 to 700. We can mark all the even numbers. The visual representation reinforces the concept of an arithmetic sequence and helps to understand the spacing between even numbers.
Applications and Extensions
Understanding how to find the number of even integers within a given range extends beyond simple arithmetic. It has applications in various fields, including:
- Computer Science: Determining the number of even addresses in memory.
- Data Analysis: Counting even-numbered entries in datasets.
- Cryptography: Certain cryptographic algorithms utilize even and odd numbers.
Furthermore, this problem can be extended to other arithmetic sequences, like finding the number of multiples of 3 or 5 within a given range. The fundamental principle remains the same: using the formula for the nth term of an arithmetic sequence.
Advanced Techniques: Summation and Series
While the arithmetic sequence method is efficient, let's explore a more advanced approach using summation. The sum of an arithmetic series can be calculated using the formula:
S = n/2 * (a₁ + aₙ)
Where:
- S is the sum of the series
- n is the number of terms
- a₁ is the first term
- aₙ is the last term
While this formula doesn't directly give us the number of terms, it can be used in conjunction with the nth term formula to solve problems related to sums of even integers within a range.
Conclusion: A Multifaceted Problem
The seemingly simple question of counting even integers between 200 and 700 allows us to explore several mathematical concepts and techniques. We've seen how direct counting, arithmetic sequences, and even summation can be utilized to arrive at the solution. Understanding the nuances of inclusive versus exclusive ranges, visualizing the problem, and recognizing the broader applications of the problem-solving methods are key takeaways. The beauty of mathematics lies in its ability to approach problems from different perspectives, and this example perfectly illustrates this versatility. Remember to clearly define your parameters and choose the method that best suits the complexity of the problem at hand. The key is not just finding the answer but understanding the underlying principles and expanding your mathematical toolkit.
Latest Posts
Latest Posts
-
3 Main Parts Of A Nucleotide
May 09, 2025
-
Why Is Blood Considered To Be A Connective Tissue
May 09, 2025
-
Name For A Group Of Penguins
May 09, 2025
-
What Is 1 Billion X 1 Trillion
May 09, 2025
-
Vinegar Is An Acid Or Base
May 09, 2025
Related Post
Thank you for visiting our website which covers about How Many Even Integers Are There Between 200 And 700 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.