How Many Bases Does A Pyramid Have
Juapaving
Mar 24, 2025 · 4 min read
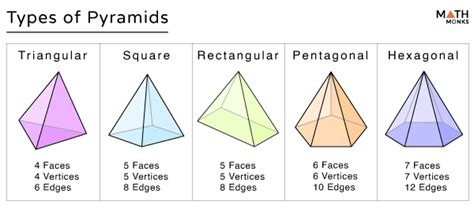
Table of Contents
How Many Bases Does a Pyramid Have? Exploring the Geometry of Pyramids
The seemingly simple question, "How many bases does a pyramid have?" opens a fascinating exploration into the geometry of pyramids, their various types, and the subtle nuances of mathematical definitions. While the immediate answer might seem obvious, a deeper dive reveals a richer understanding of these iconic structures and their mathematical representation.
Understanding the Definition of a Pyramid
Before we delve into the number of bases, let's establish a clear understanding of what constitutes a pyramid in geometry. A pyramid is a polyhedron formed by connecting a polygonal base and a point, called the apex. The lateral faces are triangles, each connecting one side of the base to the apex. The critical element here is the base, which defines the shape and properties of the entire pyramid.
The Classic Pyramid: One Base, Many Faces
The image that typically springs to mind when we think of a pyramid is the regular square pyramid. This type of pyramid has a square base and four triangular lateral faces. This is the quintessential pyramid, the one often depicted in illustrations and even referenced in popular culture. In this case, the answer is unequivocal: a regular square pyramid has one base.
Key characteristics of this classic pyramid:
- One polygonal base: A square.
- Triangular lateral faces: Four faces, all triangles.
- Apex: A single point at the top, connecting all the lateral faces.
This simple understanding forms the foundation for exploring more complex variations.
Exploring Variations: Beyond the Square Base
However, the world of pyramids extends far beyond the simple square base. The definition allows for any polygon to serve as the base. This leads to a variety of pyramid types, each with its unique characteristics:
-
Triangular Pyramid (Tetrahedron): This pyramid has a triangular base and three triangular lateral faces. It's the simplest type of pyramid, with all four faces being triangles. Again, it still possesses only one base.
-
Pentagonal Pyramid: As the name suggests, this pyramid uses a pentagon as its base. It has five triangular lateral faces. Once more, it has only one base.
-
Hexagonal Pyramid: This pyramid boasts a hexagonal base and six triangular lateral faces. The pattern continues: one base.
-
N-gonal Pyramid: This is a generalization encompassing all pyramids. It has an n-sided polygon as its base and n triangular lateral faces. Irrespective of the value of n, the pyramid still has only one base.
The Importance of the Base in Defining the Pyramid
The base isn't just a structural component; it's fundamental to the pyramid's definition and properties. The shape and size of the base dictate:
- The number of lateral faces: The number of sides in the base directly determines the number of triangular faces.
- The overall shape: The base's shape profoundly impacts the overall form of the pyramid.
- Surface area and volume calculations: Accurate calculations depend on the base's properties.
- Symmetry and geometric properties: The base’s symmetry affects the symmetry of the pyramid.
Addressing Potential Confusion: Truncated Pyramids and Other Variations
While the standard pyramid definition clearly points to a single base, some variations might initially cause confusion. For instance, a truncated pyramid is a pyramid where the apex has been cut off by a plane parallel to the base. This creates a second polygonal base, but the original structure still started with only one base. The truncated version is a derivative, not a fundamental alteration of the original definition.
Similarly, certain artistic representations or architectural structures might deviate from the strict geometric definition. However, when applying the rigorous geometric definition, the answer remains consistent: a pyramid, by its definition, has one base.
Understanding the Importance of Precise Definitions in Mathematics
The seemingly straightforward question of how many bases a pyramid has highlights the importance of precise definitions in mathematics. While our intuition might lead us to consider variations or exceptions, a clear and unambiguous definition ensures consistency and accurate mathematical reasoning. Without strict definitions, mathematical discussions become ambiguous and prone to misinterpretations.
Beyond Geometry: Pyramids in Culture and History
The enduring appeal of pyramids transcends pure geometry. These majestic structures, from the ancient Egyptian pyramids to the Mayan pyramids, hold immense cultural and historical significance. Understanding their geometry helps us appreciate not only their mathematical elegance but also their engineering marvels and their role in human history.
Understanding the fundamental geometric principles governing pyramids allows us to appreciate their enduring fascination and their significant place in both mathematics and human civilization.
Conclusion: One Base, Countless Facets
To reiterate, according to the standard geometric definition, a pyramid has only one base. While variations and artistic interpretations might blur this line, the core mathematical definition remains clear and consistent. This exploration highlights the importance of precise terminology and the rich mathematical framework underpinning these iconic structures. The apparent simplicity of the question masks a deeper appreciation of geometry and its role in understanding the world around us. The seemingly straightforward answer unveils a deeper understanding of mathematical precision and the fascinating world of geometric shapes.
Latest Posts
Latest Posts
-
Which Of The Following Is True About Hiv
Mar 28, 2025
-
In Which Situation Is The Distance Traveled Proportional To Time
Mar 28, 2025
-
Which Group Of Nonmetals Is The Most Reactive
Mar 28, 2025
-
99 Rounded To The Nearest Tenth
Mar 28, 2025
-
What Percent Is Equivalent To 3 8
Mar 28, 2025
Related Post
Thank you for visiting our website which covers about How Many Bases Does A Pyramid Have . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
