How Do You Get Radius From Diameter
Juapaving
Apr 08, 2025 · 5 min read
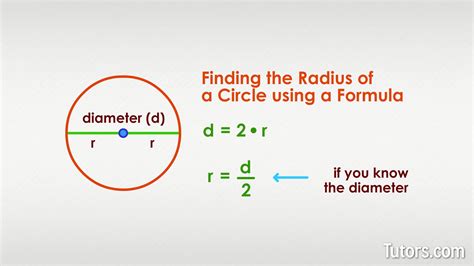
Table of Contents
How Do You Get Radius From Diameter? A Comprehensive Guide
Understanding the relationship between a circle's radius and its diameter is fundamental to geometry and numerous applications across various fields. This comprehensive guide will delve into this relationship, explaining how to calculate radius from diameter, exploring relevant formulas and concepts, and providing practical examples to solidify your understanding. We'll also touch upon the broader applications of this simple yet crucial concept.
Understanding Circles: Diameter and Radius Defined
Before diving into the calculations, let's clearly define the key terms:
-
Diameter: The diameter of a circle is the longest straight line that can be drawn across a circle, passing through the center. It essentially divides the circle into two equal halves. Think of it as a line segment that connects two points on the circle's circumference, going through the very heart of the circle – its center.
-
Radius: The radius of a circle is the distance from the center of the circle to any point on its circumference. It's essentially half the length of the diameter. It's a straight line segment connecting the center to the edge. You can draw infinitely many radii in a single circle.
The Fundamental Relationship: Radius = Diameter / 2
The core relationship between the radius (r) and the diameter (d) of a circle is incredibly straightforward:
Radius (r) = Diameter (d) / 2
This simple formula tells us that the radius is always exactly half the length of the diameter. This holds true for every circle, regardless of its size. This is a fundamental concept in geometry and forms the basis for many further calculations related to circles.
Calculating Radius from Diameter: Practical Examples
Let's illustrate this with some practical examples:
Example 1: A Simple Calculation
If a circle has a diameter of 10 cm, what is its radius?
Using the formula:
r = d / 2 = 10 cm / 2 = 5 cm
Therefore, the radius of the circle is 5 cm.
Example 2: Dealing with Decimals
A circular plate has a diameter of 7.5 inches. Find its radius.
r = d / 2 = 7.5 inches / 2 = 3.75 inches
The radius of the plate is 3.75 inches.
Example 3: Using Units of Measurement
A circular garden has a diameter of 12 meters. Calculate its radius.
r = d / 2 = 12 meters / 2 = 6 meters
The garden's radius is 6 meters. Remember to always include the units of measurement in your answer for clarity and accuracy.
Beyond Basic Calculations: Applications in Various Fields
The seemingly simple calculation of finding the radius from the diameter has wide-ranging applications in numerous fields, including:
1. Engineering and Design:
- Mechanical Engineering: Designing circular components like gears, pulleys, and shafts requires precise knowledge of radius and diameter. Calculations involving rotational speeds, torque, and stress depend heavily on these dimensions.
- Civil Engineering: Designing circular structures like tunnels, water pipes, and dome roofs relies heavily on accurate radius and diameter measurements for structural integrity and efficient material usage.
- Architectural Design: Creating circular or semi-circular architectural elements necessitates precise calculations of radii for harmonious design and structural stability.
2. Physics and Astronomy:
- Orbital Mechanics: Calculating the orbital radius of planets and satellites is crucial for understanding their motion and predicting their positions. The relationship between radius and diameter plays a pivotal role in these calculations.
- Atomic Physics: Understanding the structure of atoms often involves models based on circular orbits of electrons. The concept of radius is essential for defining these orbits.
3. Computer Graphics and Game Development:
- Creating Circular Objects: Generating circular shapes in computer graphics requires accurate radius and diameter calculations for rendering and animation.
- Collision Detection: In game development, detecting collisions between circular objects relies on precise radius calculations.
4. Manufacturing and Production:
- Manufacturing Circular Parts: Creating circular parts with specific diameters requires precise control over the radius during manufacturing processes.
- Quality Control: Measuring the radius of manufactured parts is a crucial aspect of quality control, ensuring they meet the required specifications.
5. Everyday Life:
- Cooking and Baking: Understanding circle dimensions is helpful in baking, when dealing with circular cake pans or cookie cutters. The radius helps determine the appropriate amount of batter or dough.
- Gardening and Landscaping: Planning circular flower beds or patios necessitates accurate radius and diameter calculations to ensure the desired size and shape.
Working with Circumference and Area: Expanding Your Knowledge
The radius is also fundamental to calculating other crucial characteristics of a circle:
1. Circumference:
The circumference (C) of a circle is the distance around its edge. It's calculated using the formula:
C = 2πr or C = πd
where π (pi) is approximately 3.14159. Notice how the radius (r) is directly used in this formula, making it essential for determining the circumference.
2. Area:
The area (A) of a circle is the space enclosed within its circumference. It's calculated using the formula:
A = πr²
Again, the radius (r) is the key component in this formula, showcasing its central role in determining the area of a circle.
Advanced Concepts and Further Exploration
While the basic formula for finding the radius from the diameter is simple, more advanced geometrical concepts build upon this foundation. These include:
- Inscribed and Circumscribed Circles: Understanding the relationship between circles and other shapes, such as triangles and polygons, involves using radius and diameter calculations.
- Spherical Geometry: The principles of radius and diameter extend to three-dimensional spheres, playing a crucial role in calculating the surface area and volume of spheres.
- Trigonometry and Circular Functions: Trigonometric functions (sine, cosine, tangent) are deeply connected to circles and rely heavily on the concept of radius.
Conclusion: Mastering the Radius-Diameter Relationship
The relationship between a circle's radius and diameter is a cornerstone of geometry and has far-reaching implications across diverse fields. Mastering the simple formula r = d / 2 empowers you to tackle a wide range of problems involving circles and spheres. This understanding extends beyond basic calculations and opens doors to more complex geometrical and mathematical concepts, ultimately enriching your knowledge and problem-solving skills. Remember to always practice with different examples and explore the wider applications of this fundamental geometrical concept. By grasping this seemingly simple relationship, you are unlocking a gateway to a deeper comprehension of the world around us.
Latest Posts
Latest Posts
-
How Many Feet Is 65 In
Apr 08, 2025
-
5 Letter Words Beginning With Ae
Apr 08, 2025
-
The Most Abundant Metal In The Earths Crust Is
Apr 08, 2025
-
Log 1 2 3 Log1 Log2 Log3
Apr 08, 2025
-
How Many Valence Electrons Does Alkali Metals Have
Apr 08, 2025
Related Post
Thank you for visiting our website which covers about How Do You Get Radius From Diameter . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.