Graph Of X 2 X 1
Juapaving
May 14, 2025 · 4 min read
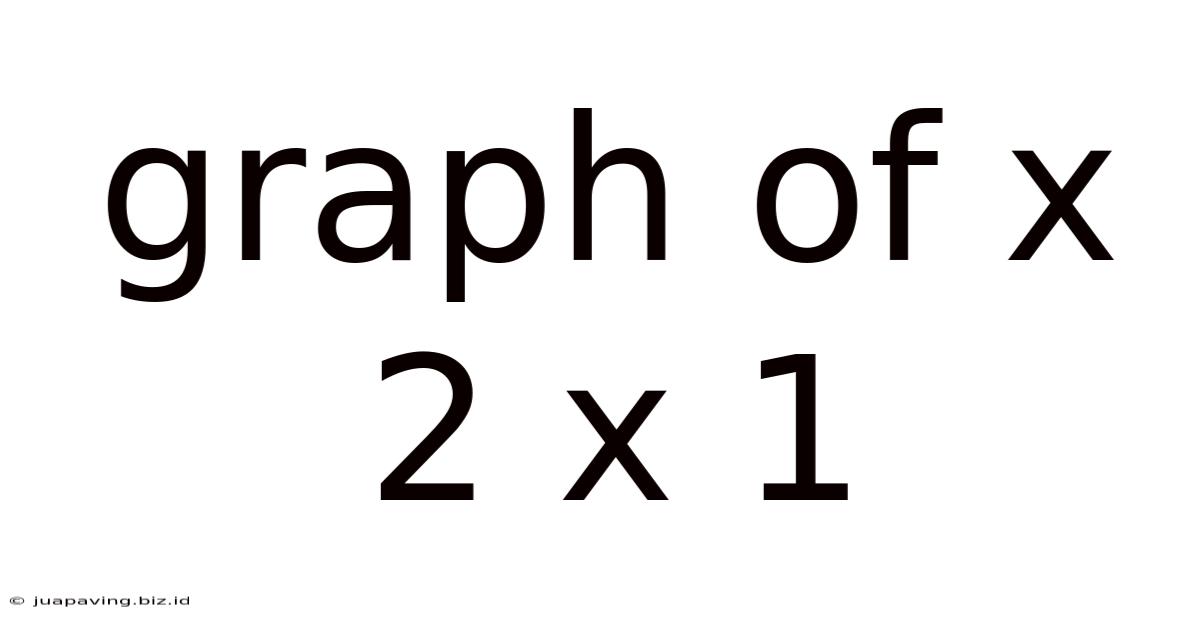
Table of Contents
Exploring the Graph of x² - x - 1: A Deep Dive into Quadratic Functions
The seemingly simple quadratic equation, x² - x - 1 = 0, hides a wealth of mathematical richness. Understanding its graph provides valuable insights into the behavior of quadratic functions, their properties, and applications in various fields. This comprehensive exploration delves into the intricacies of this specific quadratic, covering its key features, derivation methods, and practical implications.
Understanding the Basics: Quadratic Functions and Their Graphs
Before diving into the specifics of x² - x - 1, let's establish a foundational understanding of quadratic functions. A quadratic function is a polynomial function of degree two, generally represented as:
f(x) = ax² + bx + c, where a, b, and c are constants, and a ≠ 0.
The graph of a quadratic function is always a parabola, a U-shaped curve. The parabola opens upwards (concave up) if a > 0 and downwards (concave down) if a < 0. The key features of a parabola include:
- Vertex: The highest or lowest point on the parabola. For a quadratic in the form ax² + bx + c, the x-coordinate of the vertex is given by -b/(2a).
- Axis of Symmetry: A vertical line passing through the vertex, dividing the parabola into two symmetrical halves. Its equation is x = -b/(2a).
- x-intercepts (Roots): The points where the parabola intersects the x-axis (where y = 0). These are also known as the roots or zeros of the quadratic equation.
- y-intercept: The point where the parabola intersects the y-axis (where x = 0). This is simply the value of c.
Analyzing the Graph of x² - x - 1
Now, let's focus on our specific equation: x² - x - 1 = 0. In this case, a = 1, b = -1, and c = -1. Since a > 0, the parabola opens upwards.
1. Finding the Vertex
The x-coordinate of the vertex is given by -b/(2a) = -(-1)/(2*1) = 1/2.
To find the y-coordinate, we substitute x = 1/2 into the equation:
f(1/2) = (1/2)² - (1/2) - 1 = 1/4 - 1/2 - 1 = -5/4
Therefore, the vertex of the parabola is (1/2, -5/4).
2. Determining the Axis of Symmetry
The axis of symmetry is a vertical line passing through the vertex, given by the equation x = 1/2.
3. Calculating the x-intercepts (Roots)
To find the x-intercepts, we set y = 0 and solve the quadratic equation x² - x - 1 = 0. Since this equation doesn't factor easily, we can use the quadratic formula:
x = [-b ± √(b² - 4ac)] / 2a
Substituting our values, we get:
x = [1 ± √((-1)² - 4 * 1 * -1)] / 2 * 1 = [1 ± √5] / 2
Therefore, the x-intercepts are approximately x ≈ 1.618 and x ≈ -0.618. These values are related to the Golden Ratio, a fascinating mathematical constant.
4. Identifying the y-intercept
The y-intercept is the value of the function when x = 0. Substituting x = 0 into the equation, we get:
f(0) = 0² - 0 - 1 = -1
Thus, the y-intercept is (0, -1).
Graphical Representation and Key Observations
With the vertex, axis of symmetry, x-intercepts, and y-intercept determined, we can now accurately sketch the graph of x² - x - 1. The graph will be a parabola opening upwards, symmetric around the line x = 1/2, intersecting the x-axis at approximately 1.618 and -0.618, and intersecting the y-axis at -1.
Advanced Analysis: Derivatives and Concavity
Further insights into the graph's behavior can be gained by analyzing its first and second derivatives.
1. First Derivative
The first derivative, f'(x), represents the slope of the tangent line at any point on the curve. For f(x) = x² - x - 1, the first derivative is:
f'(x) = 2x - 1
Setting f'(x) = 0, we find the critical point: 2x - 1 = 0 => x = 1/2. This confirms the x-coordinate of the vertex. The first derivative helps determine where the function is increasing (f'(x) > 0) and decreasing (f'(x) < 0).
2. Second Derivative
The second derivative, f''(x), indicates the concavity of the function. For f(x) = x² - x - 1, the second derivative is:
f''(x) = 2
Since f''(x) is always positive, the function is always concave up, confirming the upward-opening parabola.
Applications and Real-World Connections
Quadratic functions, and their graphical representations, find widespread applications in various fields:
- Physics: Projectile motion, where the trajectory of a thrown object follows a parabolic path.
- Engineering: Designing parabolic antennas and reflectors, leveraging the reflective properties of parabolas.
- Economics: Modeling cost functions, revenue functions, and profit maximization.
- Computer Graphics: Creating curves and shapes in computer-aided design (CAD) software.
- Statistics: Representing distributions and fitting curves to data.
Conclusion: The Richness of a Simple Equation
The seemingly simple equation x² - x - 1 = 0 reveals a rich tapestry of mathematical concepts and practical applications. By systematically analyzing its graph, we uncover valuable insights into the behavior of quadratic functions, their properties, and their significance across various disciplines. This detailed exploration highlights the power of visual representation in understanding and applying mathematical principles. Further exploration could involve analyzing the function's behavior as x approaches infinity or negative infinity, or investigating its integral. The graph of x² - x - 1 serves as a powerful illustration of the interconnectedness of mathematical concepts and their relevance in the real world.
Latest Posts
Latest Posts
-
1 75 Liters Equals How Many Milliliters
May 14, 2025
-
What Is The Difference Between Migrant And Immigrant
May 14, 2025
-
A Quarter Is How Many Months
May 14, 2025
-
Dry Ice Is Made Of What
May 14, 2025
-
5 Letter Words Ends With An
May 14, 2025
Related Post
Thank you for visiting our website which covers about Graph Of X 2 X 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.