Find The Lcm Of 12 And 15
Juapaving
May 11, 2025 · 5 min read
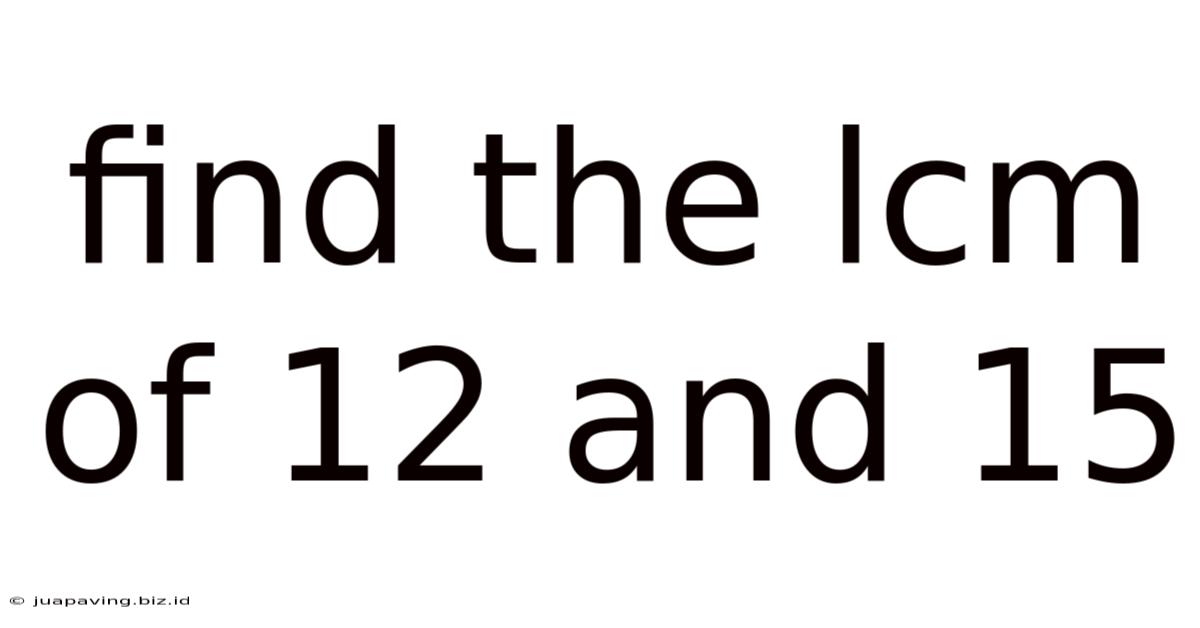
Table of Contents
Find the LCM of 12 and 15: A Comprehensive Guide
Finding the least common multiple (LCM) is a fundamental concept in mathematics, crucial for various applications from simplifying fractions to solving complex problems in algebra and number theory. This comprehensive guide will delve into the methods of finding the LCM of 12 and 15, exploring different approaches and demonstrating their applications. We'll also cover the underlying mathematical principles and provide numerous examples to solidify your understanding.
Understanding Least Common Multiple (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that contains all the integers as factors. Understanding LCM is critical for various mathematical operations, including:
- Simplifying fractions: Finding the LCM of the denominators helps in adding or subtracting fractions with different denominators.
- Solving equations: LCM is useful in solving Diophantine equations (equations where solutions must be integers).
- Scheduling problems: Determining when events with different periodicities coincide (e.g., determining when two machines will complete their cycles simultaneously).
Methods for Finding the LCM of 12 and 15
There are several effective methods to calculate the LCM of two numbers. Let's explore the most common techniques using 12 and 15 as our example:
Method 1: Listing Multiples
This method involves listing the multiples of each number until a common multiple is found. The smallest common multiple is the LCM.
Multiples of 12: 12, 24, 36, 48, 60, 72, 84, 96, 108, 120... Multiples of 15: 15, 30, 45, 60, 75, 90, 105, 120...
As we can see, the smallest common multiple of 12 and 15 is 60. Therefore, the LCM(12, 15) = 60.
This method is straightforward for smaller numbers, but it becomes less efficient for larger numbers where listing multiples can be time-consuming.
Method 2: Prime Factorization
This is a more efficient method, especially for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM from the prime factors.
Prime factorization of 12: 2² x 3 Prime factorization of 15: 3 x 5
To find the LCM using prime factorization:
- Identify the highest power of each prime factor present in the factorizations: We have 2², 3, and 5.
- Multiply these highest powers together: 2² x 3 x 5 = 4 x 3 x 5 = 60
Therefore, LCM(12, 15) = 60. This method is generally preferred for its efficiency and systematic approach.
Method 3: Using the Formula: LCM(a, b) = (|a x b|) / GCD(a, b)
This method utilizes the greatest common divisor (GCD) of the two numbers. The GCD is the largest number that divides both integers without leaving a remainder. We can use the Euclidean algorithm to find the GCD.
Finding the GCD of 12 and 15 using the Euclidean algorithm:
- Divide the larger number (15) by the smaller number (12): 15 ÷ 12 = 1 with a remainder of 3.
- Replace the larger number with the smaller number (12) and the smaller number with the remainder (3): 12 ÷ 3 = 4 with a remainder of 0.
- The last non-zero remainder is the GCD, which is 3. Therefore, GCD(12, 15) = 3.
Now, we can use the formula:
LCM(12, 15) = (|12 x 15|) / GCD(12, 15) = (180) / 3 = 60
This method is highly efficient and provides a direct calculation, particularly useful for larger numbers where prime factorization might be more challenging.
Applications of LCM
The LCM has numerous applications across various fields:
1. Fraction Addition and Subtraction
When adding or subtracting fractions with different denominators, finding the LCM of the denominators is crucial to obtain a common denominator. For example:
1/12 + 1/15 = (5/60) + (4/60) = 9/60 = 3/20
Here, the LCM of 12 and 15 (60) is used to find the common denominator.
2. Cyclic Events
LCM is frequently used to solve problems involving cyclical events. For instance, if two machines complete cycles every 12 and 15 minutes respectively, the LCM (60) determines when they will complete their cycles simultaneously. This is useful in scheduling and production planning.
3. Number Theory and Cryptography
The LCM plays a significant role in number theory, including modular arithmetic and cryptography. It's fundamental in solving certain types of Diophantine equations and constructing RSA encryption algorithms.
4. Music Theory
In music, the LCM helps determine the least common denominator for rhythmic patterns and note values, facilitating harmonic analysis and composition.
Beyond the Basics: LCM of More Than Two Numbers
The methods discussed above can be extended to find the LCM of more than two numbers. For example, to find the LCM of 12, 15, and 20:
Prime factorization method:
12 = 2² x 3 15 = 3 x 5 20 = 2² x 5
The highest powers are 2², 3, and 5. Therefore, LCM(12, 15, 20) = 2² x 3 x 5 = 60.
Conclusion: Mastering LCM Calculations
Understanding and efficiently calculating the least common multiple is a valuable skill in mathematics. This guide has explored multiple methods for finding the LCM, focusing specifically on the LCM of 12 and 15, while also highlighting broader applications. Whether using the listing multiples method, prime factorization, or the GCD-based formula, choosing the most appropriate technique depends on the complexity of the numbers involved. Mastering these methods provides a solid foundation for tackling more advanced mathematical problems. Remember to practice regularly to reinforce your understanding and improve your efficiency in LCM calculations. The ability to quickly and accurately find the LCM will prove invaluable in various mathematical contexts and practical applications.
Latest Posts
Latest Posts
-
Adjectives That Start With A V
May 12, 2025
-
What Is The Least Common Multiple Of 32 And 48
May 12, 2025
-
Cells That Are Not Dividing Remain In The
May 12, 2025
-
In Which Stage Of Meiosis Crossing Over Occurs
May 12, 2025
-
How Many Edges Does Cuboid Has
May 12, 2025
Related Post
Thank you for visiting our website which covers about Find The Lcm Of 12 And 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.