Find The Gcf Of 8 And 12
Juapaving
Apr 08, 2025 · 5 min read
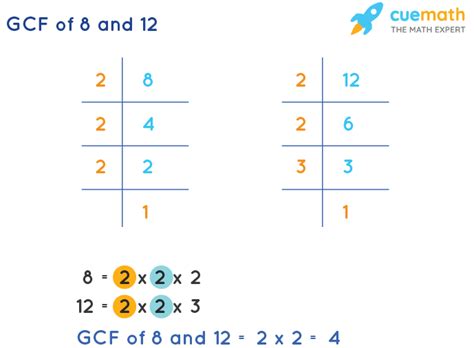
Table of Contents
Finding the Greatest Common Factor (GCF) of 8 and 12: A Comprehensive Guide
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers is a fundamental concept in mathematics. It's a crucial skill for simplifying fractions, solving algebraic equations, and understanding number theory. This comprehensive guide will explore various methods for finding the GCF of 8 and 12, explaining the process in detail and providing examples to solidify your understanding. We’ll move beyond simply finding the GCF and delve into the broader applications and significance of this mathematical concept.
Understanding the Greatest Common Factor (GCF)
Before we dive into the methods for finding the GCF of 8 and 12, let's define what a GCF actually is. The GCF of two or more numbers is the largest number that divides evenly into all of the given numbers without leaving a remainder. In simpler terms, it's the biggest number that is a factor of all the numbers in the set.
For example, the factors of 8 are 1, 2, 4, and 8. The factors of 12 are 1, 2, 3, 4, 6, and 12. The common factors of 8 and 12 are 1, 2, and 4. The greatest of these common factors is 4. Therefore, the GCF of 8 and 12 is 4.
Method 1: Listing Factors
This method is straightforward and works well for smaller numbers. It involves listing all the factors of each number and then identifying the largest factor that appears in both lists.
Steps:
- List the factors of 8: 1, 2, 4, 8
- List the factors of 12: 1, 2, 3, 4, 6, 12
- Identify the common factors: 1, 2, 4
- Select the greatest common factor: 4
Therefore, the GCF of 8 and 12 using the listing factors method is 4. This method is simple to understand and visualize, especially for beginners. However, it becomes less efficient when dealing with larger numbers.
Method 2: Prime Factorization
Prime factorization is a more efficient method for finding the GCF, especially when dealing with larger numbers. It involves expressing each number as a product of its prime factors. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself.
Steps:
- Find the prime factorization of 8: 8 = 2 x 2 x 2 = 2³
- Find the prime factorization of 12: 12 = 2 x 2 x 3 = 2² x 3
- Identify the common prime factors: Both numbers share two factors of 2 (2²)
- Multiply the common prime factors: 2 x 2 = 4
Therefore, the GCF of 8 and 12 using prime factorization is 4. This method is more systematic and efficient than listing all the factors, especially for larger numbers. It provides a deeper understanding of the number's composition.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, particularly useful for larger numbers where listing factors or prime factorization becomes cumbersome. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal.
Steps:
- Start with the larger number (12) and the smaller number (8): 12 and 8
- Divide the larger number by the smaller number and find the remainder: 12 ÷ 8 = 1 with a remainder of 4
- Replace the larger number with the smaller number (8) and the smaller number with the remainder (4): 8 and 4
- Repeat the process: 8 ÷ 4 = 2 with a remainder of 0
- The GCF is the last non-zero remainder: 4
Therefore, the GCF of 8 and 12 using the Euclidean algorithm is 4. This method is particularly efficient for larger numbers because it avoids the need for complete prime factorization.
Choosing the Right Method
The best method for finding the GCF depends on the numbers involved and your comfort level with different mathematical approaches.
- Listing factors: Best for small numbers where you can easily list all the factors.
- Prime factorization: More efficient for larger numbers and provides a deeper understanding of number composition.
- Euclidean algorithm: Most efficient for very large numbers, particularly when prime factorization becomes computationally intensive.
Applications of Finding the GCF
The concept of the GCF extends far beyond simple arithmetic exercises. It has numerous applications in various areas of mathematics and beyond:
-
Simplifying Fractions: The GCF is used to simplify fractions to their lowest terms. For example, the fraction 12/8 can be simplified to 3/2 by dividing both the numerator and denominator by their GCF (4).
-
Solving Algebraic Equations: The GCF plays a crucial role in factoring polynomials, a key step in solving many algebraic equations.
-
Number Theory: The GCF is a fundamental concept in number theory, used in various theorems and proofs.
-
Real-World Applications: GCF finds applications in various real-world scenarios like dividing objects or resources equally, determining the size of the largest square tile that can be used to cover a rectangular area, or optimizing resource allocation problems.
Extending the Concept: GCF of More Than Two Numbers
The methods described above can be extended to find the GCF of more than two numbers. For example, to find the GCF of 8, 12, and 16:
-
Prime Factorization:
- 8 = 2³
- 12 = 2² x 3
- 16 = 2⁴
- The common prime factor is 2², so the GCF is 4.
-
Euclidean Algorithm (can be adapted but less straightforward): The Euclidean algorithm is more complex to apply directly to multiple numbers. It's generally more efficient to find the GCF of two numbers at a time, then the GCF of the result and the next number, and so on.
Conclusion: Mastering GCF for Mathematical Proficiency
Finding the greatest common factor is a fundamental skill in mathematics with far-reaching applications. Understanding the different methods – listing factors, prime factorization, and the Euclidean algorithm – empowers you to choose the most efficient approach depending on the context. Mastering this concept not only strengthens your arithmetic skills but also provides a foundational understanding for more advanced mathematical concepts and real-world problem-solving. Regular practice with various numbers will solidify your understanding and improve your proficiency in this essential mathematical skill. Remember to choose the method best suited to the numbers you are working with, and always double-check your answers to ensure accuracy.
Latest Posts
Latest Posts
-
Two Angles That Have The Same Measure
Apr 08, 2025
-
Adjectives That Start With The Letter D
Apr 08, 2025
-
Functional Group With A Face Funny
Apr 08, 2025
-
What Do You Call A Group Of Lions
Apr 08, 2025
-
Whats The Lcm Of 9 And 12
Apr 08, 2025
Related Post
Thank you for visiting our website which covers about Find The Gcf Of 8 And 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.