Find The Area Of The Triangle Shown
Juapaving
Apr 03, 2025 · 5 min read
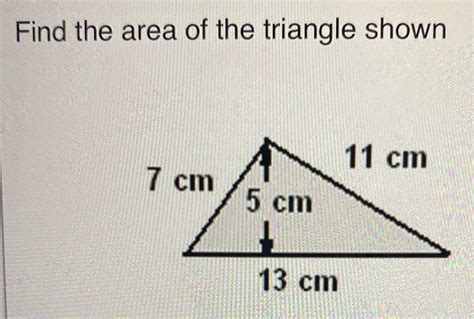
Table of Contents
Find the Area of a Triangle: A Comprehensive Guide
Finding the area of a triangle might seem like a simple task, especially from your school days. However, the methods for calculating this area vary depending on the information provided. This comprehensive guide will delve into various approaches, equipping you with the knowledge to tackle any triangle area problem, regardless of its complexity. We'll explore both basic and advanced techniques, ensuring you master this fundamental geometric concept.
Understanding the Basics: The Formula We All Know
The most common formula for calculating the area of a triangle is:
Area = (1/2) * base * height
Where:
- base: The length of one side of the triangle.
- height: The perpendicular distance from the base to the opposite vertex (the highest point).
This formula is straightforward when you're given the base and height directly. Let's look at a simple example:
Example 1: Given Base and Height
Imagine a triangle with a base of 6 cm and a height of 4 cm. Using the formula:
Area = (1/2) * 6 cm * 4 cm = 12 cm²
When the Height Isn't Directly Given: Alternative Approaches
Things get a little more interesting when the height isn't explicitly stated. This often occurs in real-world scenarios or more complex geometric problems. Let's explore several alternative methods:
Using Heron's Formula: Perfect for Three Sides
Heron's formula is a powerful tool when you know the lengths of all three sides of the triangle (a, b, and c). It's particularly useful when you can't easily determine the height. The formula works as follows:
-
Calculate the semi-perimeter (s): s = (a + b + c) / 2
-
Apply Heron's Formula: Area = √[s(s - a)(s - b)(s - c)]
Example 2: Using Heron's Formula
Let's say we have a triangle with sides a = 5 cm, b = 6 cm, and c = 7 cm.
-
Semi-perimeter (s): s = (5 + 6 + 7) / 2 = 9 cm
-
Heron's Formula: Area = √[9(9 - 5)(9 - 6)(9 - 7)] = √[9 * 4 * 3 * 2] = √216 ≈ 14.7 cm²
Using Trigonometry: When Angles and Sides Combine
Trigonometry provides another elegant solution when you have the length of two sides and the included angle. The formula utilizes the sine function:
Area = (1/2) * a * b * sin(C)
Where:
- a and b are the lengths of two sides.
- C is the angle between sides a and b.
Example 3: Using Trigonometry
Consider a triangle with sides a = 8 cm and b = 10 cm, and the angle C between them is 30 degrees.
Area = (1/2) * 8 cm * 10 cm * sin(30°) = 40 cm² * 0.5 = 20 cm²
Advanced Techniques and Special Cases
Let's delve into some more advanced scenarios and special triangle types:
Equilateral Triangles: A Simple Shortcut
Equilateral triangles have all three sides equal in length. Calculating the area is simplified using the following formula:
Area = (√3/4) * a²
Where 'a' is the length of one side.
Example 4: Equilateral Triangle
If an equilateral triangle has sides of 6 cm, the area is:
Area = (√3/4) * 6² = 9√3 cm² ≈ 15.6 cm²
Right-Angled Triangles: The Easiest Scenario (Often)
Right-angled triangles have one angle equal to 90 degrees. The two shorter sides (legs) act as the base and height, making the area calculation exceptionally easy:
Area = (1/2) * leg1 * leg2
Example 5: Right-Angled Triangle
A right-angled triangle with legs of 5 cm and 12 cm has an area of:
Area = (1/2) * 5 cm * 12 cm = 30 cm²
Coordinate Geometry: Triangles on a Plane
When triangles are defined by their vertices' coordinates on a Cartesian plane (x, y), we can use the determinant method:
Area = (1/2) |(x₁ (y₂ - y₃) + x₂ (y₃ - y₁) + x₃ (y₁ - y₂))|
Where (x₁, y₁), (x₂, y₂), and (x₃, y₃) are the coordinates of the vertices.
Example 6: Coordinate Geometry
Let's say the vertices are A(1, 2), B(4, 6), and C(7, 2).
Area = (1/2) |(1(6 - 2) + 4(2 - 2) + 7(2 - 6))| = (1/2) |4 + 0 - 28| = (1/2) |-24| = 12 square units
Choosing the Right Method: A Practical Guide
The choice of method depends entirely on the information available:
- Base and Height: Use the basic formula (1/2) * base * height.
- Three Sides: Employ Heron's formula.
- Two Sides and Included Angle: Use the trigonometric formula.
- Equilateral Triangle: Utilize the simplified formula (√3/4) * a².
- Right-Angled Triangle: Use (1/2) * leg1 * leg2.
- Coordinates of Vertices: Apply the determinant method.
Troubleshooting Common Mistakes
Even experienced mathematicians can make mistakes. Here are some common errors to watch out for:
- Incorrect Height: Ensure you are using the perpendicular height, not the slant height.
- Unit Consistency: Always use the same units throughout your calculations (cm, meters, inches, etc.).
- Rounding Errors: Be mindful of rounding errors, especially when using trigonometric functions or square roots. Carry as many significant figures as possible during intermediate steps.
- Sign Errors: When using the determinant method in coordinate geometry, pay close attention to signs.
Practical Applications: Beyond the Textbook
Understanding how to calculate triangle areas extends beyond the classroom. Its applications are vast, including:
- Surveying: Determining land areas.
- Architecture and Engineering: Calculating roof areas, structural supports, and other design elements.
- Computer Graphics: Rendering 2D and 3D shapes and scenes.
- Physics: Calculating forces, vectors, and other physical quantities.
Conclusion: Mastering Triangle Area Calculations
Finding the area of a triangle is a fundamental skill with practical applications in various fields. By understanding the different methods and choosing the appropriate approach based on the available information, you can confidently tackle any triangle area calculation. Remember to practice regularly to solidify your understanding and refine your problem-solving skills. With consistent effort, mastering this essential geometric concept will become second nature. Now go forth and calculate!
Latest Posts
Latest Posts
-
Evaporation Of Water Endothermic Or Exothermic
Apr 04, 2025
-
Difference Between Real And Natural Numbers
Apr 04, 2025
-
What Energy Conversion Occurs During Photosynthesis
Apr 04, 2025
-
How Are Fish Able To Live In A Frozen Lake
Apr 04, 2025
-
How Many Minutes Are In 9 Hours
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about Find The Area Of The Triangle Shown . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
