Find Lcm Of 3 And 4
Juapaving
May 13, 2025 · 5 min read
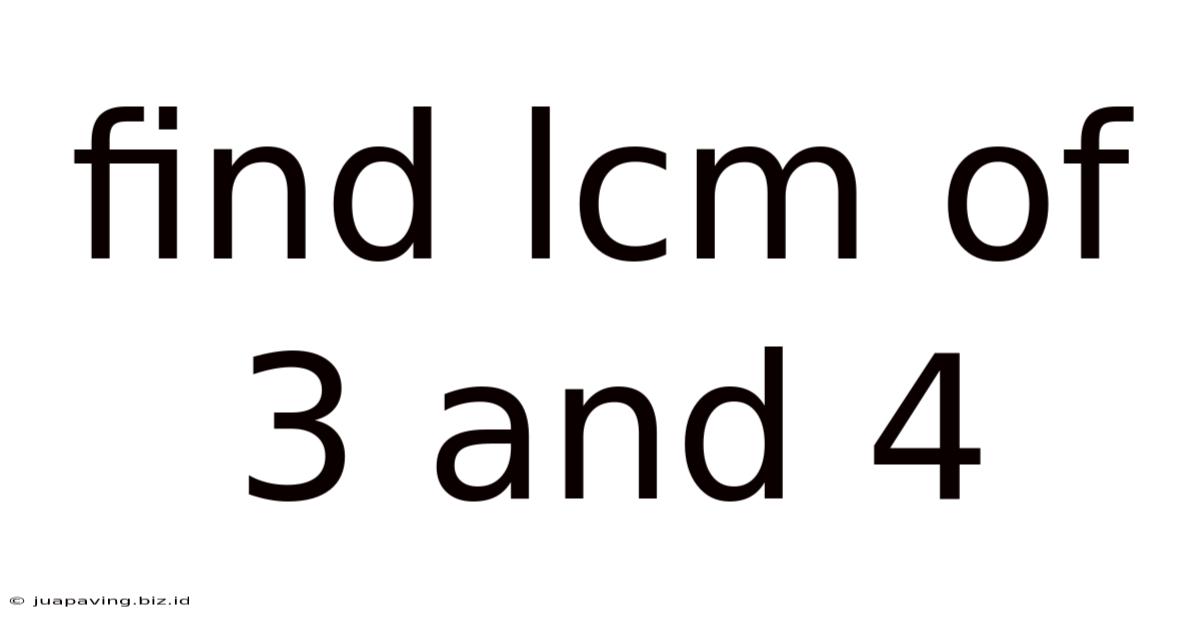
Table of Contents
Finding the LCM of 3 and 4: A Comprehensive Guide
Finding the least common multiple (LCM) of two numbers is a fundamental concept in mathematics with applications spanning various fields, from scheduling problems to music theory. This comprehensive guide will delve into the process of finding the LCM of 3 and 4, exploring multiple methods and providing a deeper understanding of the underlying principles. We'll also examine the broader context of LCMs and their significance.
Understanding Least Common Multiples (LCMs)
Before we tackle the specific problem of finding the LCM of 3 and 4, let's establish a solid understanding of what an LCM actually is. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers. Think of it as the smallest number that contains all the numbers as factors.
For example, consider the numbers 2 and 3. The multiples of 2 are 2, 4, 6, 8, 10, 12... and the multiples of 3 are 3, 6, 9, 12, 15... The common multiples are 6, 12, 18... The smallest of these common multiples is 6, so the LCM(2,3) = 6.
Method 1: Listing Multiples
This is the most straightforward method, particularly useful for smaller numbers like 3 and 4. We simply list the multiples of each number until we find the smallest common multiple.
Multiples of 3: 3, 6, 9, 12, 15, 18...
Multiples of 4: 4, 8, 12, 16, 20...
By comparing the lists, we can see that the smallest common multiple is 12. Therefore, LCM(3,4) = 12.
This method is effective for small numbers but becomes less practical as the numbers get larger. Imagine trying to list the multiples of 123 and 456! That's where more efficient methods come in.
Method 2: Prime Factorization
Prime factorization is a powerful technique for finding the LCM of any two (or more) numbers. It involves breaking down each number into its prime factors – numbers that are only divisible by 1 and themselves.
Prime Factorization of 3: 3 (3 is a prime number)
Prime Factorization of 4: 2 x 2 = 2²
Once we have the prime factorizations, we follow these steps:
- Identify the unique prime factors: In this case, the unique prime factors are 2 and 3.
- Take the highest power of each unique prime factor: The highest power of 2 is 2², and the highest power of 3 is 3¹.
- Multiply the highest powers together: 2² x 3 = 4 x 3 = 12
Therefore, the LCM(3,4) = 12, confirming the result obtained using the listing method. This method is significantly more efficient for larger numbers because it avoids the tedious process of listing multiples.
Method 3: Using the Formula (LCM and GCD Relationship)
The least common multiple (LCM) and the greatest common divisor (GCD) of two numbers are intimately related. There's a formula that connects them:
LCM(a, b) x GCD(a, b) = a x b
Where 'a' and 'b' are the two numbers. To use this method, we first need to find the GCD of 3 and 4.
The greatest common divisor (GCD) is the largest number that divides both numbers without leaving a remainder. For 3 and 4, the only common divisor is 1. Therefore, GCD(3,4) = 1.
Now, we can use the formula:
LCM(3, 4) x GCD(3, 4) = 3 x 4 LCM(3, 4) x 1 = 12 LCM(3, 4) = 12
This method elegantly links the LCM and GCD, providing another efficient way to calculate the LCM. Finding the GCD often involves the Euclidean algorithm, which is particularly helpful for larger numbers.
Method 4: Venn Diagram Approach (For Visual Learners)
While less commonly used for just two numbers, the Venn diagram method offers a visual representation of the prime factorization process, making it easier to understand, especially for beginners.
- Prime Factorize each number: As before, 3 = 3 and 4 = 2 x 2.
- Represent factors in a Venn diagram: Draw two overlapping circles, one for 3 and one for 4. Place the prime factors in the appropriate sections. Since 3 and 4 share no common factors, the overlapping section is empty.
- Calculate the LCM: Multiply the factors in each section, including the overlapping (empty in this case). The product is 3 x 2 x 2 = 12.
This visual approach helps solidify the concept of finding the LCM through prime factorization.
Real-World Applications of LCM
The concept of LCM has far-reaching applications in various fields:
- Scheduling: Imagine two buses leaving a depot at different intervals. Finding the LCM of their intervals helps determine when they will depart at the same time again.
- Music Theory: LCM is crucial in music for determining the least common multiple of the note durations, influencing harmony and rhythm.
- Construction: LCM helps coordinate tasks that need to be completed at synchronized intervals, ensuring efficiency.
- Computer Science: In algorithms and data structures, the LCM often arises in problems related to synchronization and cycle detection.
- Everyday Life: Simple scenarios, like dividing cookies evenly among children with different numbers of cookies per pack, also involve LCM principles.
Expanding to More Than Two Numbers
The methods discussed above, especially prime factorization, can be readily extended to find the LCM of more than two numbers. For example, to find the LCM of 3, 4, and 5:
- Prime Factorization: 3 = 3, 4 = 2², 5 = 5
- Unique Prime Factors: 2, 3, 5
- Highest Powers: 2², 3¹, 5¹
- Multiply: 2² x 3 x 5 = 4 x 3 x 5 = 60
Therefore, LCM(3, 4, 5) = 60.
Conclusion: Mastering LCM Calculations
Finding the LCM of 3 and 4, while seemingly simple, provides a foundation for understanding this crucial mathematical concept. Whether you use the listing method, prime factorization, the LCM/GCD formula, or the Venn diagram approach, the key is to choose the method best suited to the numbers involved and your level of understanding. Remember, mastering LCM calculations opens doors to a deeper appreciation of mathematical relationships and their applications in various aspects of life. This comprehensive guide has equipped you with the knowledge and tools to confidently tackle LCM problems of increasing complexity. Practice is key – so try finding the LCM of different number pairs and sets to solidify your understanding!
Latest Posts
Latest Posts
-
The Force That Opposes Motion Is Called
May 13, 2025
-
Which Image Represents Cytokinesis In A Plant Cell
May 13, 2025
-
Line Passes Through The Point And Has A Slope Of
May 13, 2025
-
What Do You Call A Seven Sided Shape
May 13, 2025
-
Como Se Dice 137 En Ingles
May 13, 2025
Related Post
Thank you for visiting our website which covers about Find Lcm Of 3 And 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.