Find Area And Perimeter Of A Triangle
Juapaving
Apr 06, 2025 · 5 min read
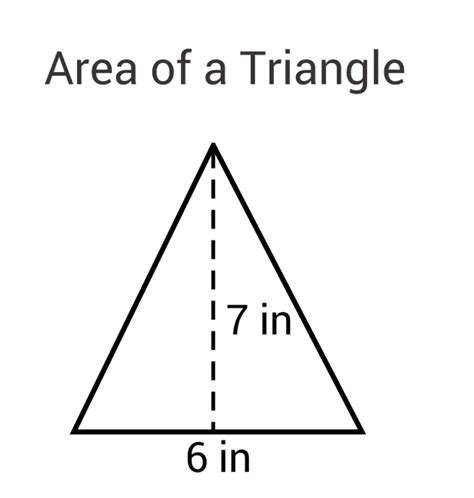
Table of Contents
Find Area and Perimeter of a Triangle: A Comprehensive Guide
Understanding how to calculate the area and perimeter of a triangle is fundamental in geometry and has numerous practical applications in various fields, from architecture and engineering to surveying and computer graphics. This comprehensive guide will delve into the different methods for calculating both area and perimeter, catering to different types of triangles and levels of mathematical understanding. We'll cover everything from basic formulas to more advanced techniques, ensuring you develop a solid grasp of this essential geometrical concept.
Understanding Triangles: Types and Properties
Before diving into the calculations, let's establish a firm foundation by reviewing the different types of triangles and their key properties. Triangles are classified based on their sides and angles:
Classification by Sides:
- Equilateral Triangle: All three sides are equal in length. This also implies that all three angles are equal (60 degrees each).
- Isosceles Triangle: Two sides are equal in length. The angles opposite these equal sides are also equal.
- Scalene Triangle: All three sides are of different lengths. Consequently, all three angles are also different.
Classification by Angles:
- Acute Triangle: All three angles are less than 90 degrees.
- Right-angled Triangle: One angle is exactly 90 degrees (a right angle).
- Obtuse Triangle: One angle is greater than 90 degrees.
Understanding these classifications is crucial because the methods for calculating area and perimeter may vary slightly depending on the type of triangle.
Calculating the Perimeter of a Triangle
The perimeter of any polygon, including a triangle, is simply the total length of its sides. For a triangle with sides a, b, and c, the perimeter (P) is calculated using the following formula:
P = a + b + c
This formula is universally applicable to all types of triangles – equilateral, isosceles, and scalene. Simply measure or determine the length of each side and add them together.
Example:
Let's say we have a triangle with sides measuring 5 cm, 7 cm, and 9 cm. The perimeter would be:
P = 5 cm + 7 cm + 9 cm = 21 cm
Calculating the Area of a Triangle
Calculating the area of a triangle is slightly more complex than finding its perimeter, and the method used depends on the information available. Here are the most common approaches:
1. Using Base and Height (Most Common Method):
This is the most widely used method and works for all types of triangles. The formula is:
Area = (1/2) * base * height
Where:
- base: The length of any one side of the triangle.
- height: The perpendicular distance from the base to the opposite vertex (the highest point).
Important Note: The height is not necessarily a side of the triangle. It's the perpendicular line segment drawn from the vertex to the base (or its extension).
Example:
Imagine a triangle with a base of 10 cm and a height of 6 cm. The area would be:
Area = (1/2) * 10 cm * 6 cm = 30 cm²
2. Heron's Formula (When Side Lengths are Known):
Heron's formula is particularly useful when you know the lengths of all three sides of the triangle but don't know the height. It's applicable to all types of triangles.
First, calculate the semi-perimeter (s):
s = (a + b + c) / 2
Where a, b, and c are the lengths of the three sides.
Then, use Heron's formula to calculate the area:
Area = √[s(s - a)(s - b)(s - c)]
Example:
Consider a triangle with sides of 5 cm, 6 cm, and 7 cm.
-
Calculate the semi-perimeter: s = (5 + 6 + 7) / 2 = 9 cm
-
Apply Heron's formula: Area = √[9(9 - 5)(9 - 6)(9 - 7)] = √[9 * 4 * 3 * 2] = √216 ≈ 14.7 cm²
3. Using Trigonometry (For Right-Angled Triangles and When Angles are Known):
If you know the lengths of two sides and the included angle of a triangle, you can use trigonometry to find the area. This is particularly helpful for right-angled triangles. The formula is:
Area = (1/2) * a * b * sin(C)
Where:
- a and b are the lengths of two sides.
- C is the angle between sides a and b.
Example:
For a right-angled triangle with sides a = 8 cm, b = 6 cm, and angle C = 90 degrees (sin 90° = 1):
Area = (1/2) * 8 cm * 6 cm * sin(90°) = 24 cm²
Advanced Applications and Real-World Examples
The ability to calculate the area and perimeter of a triangle extends far beyond simple geometric exercises. Here are some real-world applications:
1. Surveying and Land Measurement:
Surveyors frequently utilize triangular measurements to determine land areas. By measuring the lengths of the sides of a triangular plot of land, they can accurately calculate its area using Heron's formula.
2. Architecture and Construction:
In architecture and construction, calculating triangular areas is essential for determining the amount of materials needed for roofing, window panes, or other triangular components of a building.
3. Engineering:
Engineers use triangle calculations in various structural designs, particularly in frameworks and trusses. The strength and stability of these structures depend on precise calculations of triangular areas and perimeters.
4. Computer Graphics and Game Development:
In computer graphics and game development, triangles are the fundamental building blocks of 3D models. Calculating the area and perimeter of these triangles is crucial for rendering images and simulating realistic physics.
5. Navigation:
Triangulation, a technique employing triangles, is widely used in navigation systems like GPS to determine the precise location of objects or vehicles.
Conclusion: Mastering Triangle Calculations
Mastering the calculation of the area and perimeter of a triangle is a valuable skill with wide-ranging applications. By understanding the different formulas and approaches, you equip yourself with the tools to tackle a variety of geometrical problems and contribute to practical solutions in various fields. Remember to choose the most appropriate formula based on the information available about the triangle (side lengths, angles, or height). Practice applying these formulas to different triangle types to solidify your understanding. This guide serves as a starting point for a deeper exploration of geometric calculations and their real-world significance. With continued practice and exploration, your proficiency in this crucial area of geometry will only improve.
Latest Posts
Latest Posts
-
How Many Feet Is 17 Inches
Apr 07, 2025
-
How Many Feet Is 14 Inches
Apr 07, 2025
-
Is Capacity And Volume The Same
Apr 07, 2025
-
Is Potassium Oxide Ionic Or Covalent
Apr 07, 2025
-
6 Quarts Is How Many Cups
Apr 07, 2025
Related Post
Thank you for visiting our website which covers about Find Area And Perimeter Of A Triangle . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
