Equilateral Triangle Inscribed In A Circle
Juapaving
Apr 07, 2025 · 5 min read
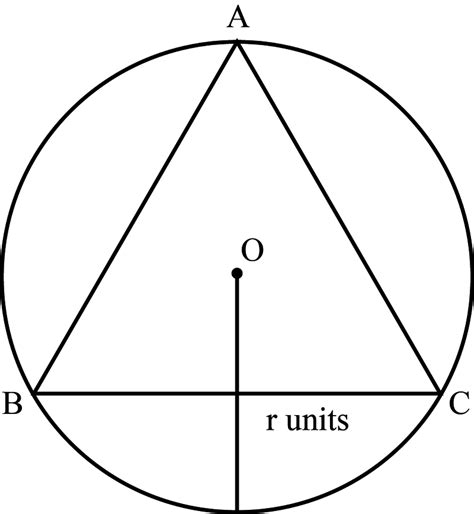
Table of Contents
Equilateral Triangle Inscribed in a Circle: A Deep Dive into Geometry and its Applications
The elegant symmetry of an equilateral triangle perfectly inscribed within a circle has captivated mathematicians and geometers for centuries. This seemingly simple geometric configuration holds a wealth of fascinating properties and relationships, leading to numerous applications in various fields. This article delves into the intricacies of this geometric marvel, exploring its key features, derivations, and practical implications.
Understanding the Fundamentals
Before embarking on a detailed exploration, let's establish a firm understanding of the core components:
-
Equilateral Triangle: A triangle with all three sides of equal length and all three angles measuring 60 degrees. Its inherent symmetry is a key characteristic.
-
Inscribed Triangle: A triangle whose vertices all lie on the circumference of a circle. The circle is then said to circumscribe the triangle.
-
Circumcircle: The circle that passes through all three vertices of a triangle. Its center is the circumcenter, and its radius is the circumradius.
The combination of these elements creates a unique geometric relationship, characterized by harmonious proportions and intriguing mathematical connections. This relationship isn't arbitrary; it's governed by precise geometrical laws.
Deriving Key Properties
Several key properties govern the relationship between an equilateral triangle and its circumcircle. Let's explore some of the most significant ones:
1. The Circumcenter and Centroid Coincidence
In an equilateral triangle, the circumcenter (the center of the circumcircle), the centroid (the intersection of the medians), and the orthocenter (the intersection of the altitudes) all coincide at a single point. This point is also the incenter (the center of the inscribed circle). This unique confluence of geometric centers is a defining characteristic of equilateral triangles, setting them apart from other types of triangles. This remarkable property greatly simplifies many calculations and geometric constructions related to the inscribed equilateral triangle.
2. Relationship between Side Length and Circumradius
Let's denote the side length of the equilateral triangle as 's' and the radius of the circumcircle as 'R'. A fundamental relationship exists between these two quantities:
R = s / √3
This formula provides a direct and elegant connection between the dimensions of the triangle and its circumscribing circle. Given either the side length or the circumradius, one can easily calculate the other. This simple yet powerful equation is frequently used in various geometric problems and applications.
3. Angle Subtended at the Circumference
Each side of the inscribed equilateral triangle subtends an angle of 120 degrees at the circumference of the circle. This is a direct consequence of the 60-degree interior angles of the equilateral triangle. The angles subtended at the circumference are twice the magnitude of the angles subtended at the center. This relationship is a crucial concept in understanding cyclic quadrilaterals and other geometric configurations involving inscribed figures.
4. Area Relationship
The area of an equilateral triangle inscribed in a circle is directly related to the circumradius. The area (A) can be expressed as:
A = (3√3/4) * R²
This formula highlights the elegant interplay between the area of the triangle and the radius of its circumcircle, offering a concise way to calculate the area given the circumradius, or vice versa. This is especially useful in applications where the circumradius is readily available or easier to determine than the side length of the triangle.
Applications and Significance
The properties of an equilateral triangle inscribed in a circle have far-reaching applications in various fields:
1. Engineering and Design
The inherent symmetry and predictable relationships within this geometric configuration are utilized in:
-
Structural Engineering: The equilateral triangle's stability and strength are leveraged in bridge design, tower construction, and other structural applications. The inherent rigidity of the equilateral triangle distributes stress effectively, making it a suitable choice for load-bearing structures.
-
Mechanical Design: The geometric properties are used in the design of gear systems, linkages, and other mechanical components. The predictable angles and distances facilitate precise calculations of movement and force transmission.
-
Architectural Design: The aesthetically pleasing symmetry of the equilateral triangle and its relationship with the circle are often integrated into architectural designs, offering both structural integrity and visual appeal.
2. Computer Graphics and Animation
The precise mathematical relationships governing the equilateral triangle inscribed within a circle are exploited in:
-
Computer-Aided Design (CAD): The accurate and efficient generation of equilateral triangles and their circumcircles is essential in various CAD applications. The properties discussed provide algorithms for creating and manipulating these shapes with precision.
-
3D Modeling and Animation: The symmetry and predictable properties simplify the creation and manipulation of 3D models and animations involving equilateral triangles and rotational symmetry.
3. Mathematics and Geometry
The equilateral triangle inscribed in a circle serves as a fundamental element in:
-
Trigonometry: It provides a visual and intuitive representation of trigonometric functions and identities.
-
Geometric Constructions: It's a key building block in many geometric constructions and proofs.
-
Higher-Level Mathematics: The properties of inscribed equilateral triangles find their way into more advanced mathematical concepts, demonstrating the far-reaching impact of this fundamental geometric relationship.
Beyond the Basics: Further Exploration
This exploration of the equilateral triangle inscribed in a circle only scratches the surface. Further investigation can involve:
-
Exploring the relationship with other inscribed figures: How does this configuration relate to inscribed squares, pentagons, or other polygons? The comparative analysis of different inscribed shapes within the same circle reveals interesting geometric relationships.
-
Examining the effects of transformations: How are the properties of the inscribed equilateral triangle affected by rotations, reflections, or dilations? Understanding these transformations provides further insight into the inherent symmetries and properties of the configuration.
-
Investigating applications in other fields: Are there applications in fields like physics, chemistry, or even music theory that leverage the unique properties of this geometric configuration? The exploration of unconventional applications can reveal unexpected connections and insights.
Conclusion
The seemingly simple configuration of an equilateral triangle inscribed in a circle reveals a rich tapestry of mathematical relationships and practical applications. Its inherent symmetry, predictable properties, and elegant formulas have captivated mathematicians and influenced various fields for centuries. From structural engineering to computer graphics, the understanding and application of this geometric marvel continue to be relevant and vital in our technological world. The continuing exploration of its properties promises further insights and discoveries, solidifying its position as a fundamental concept in geometry and beyond. The inherent beauty and utility of this simple yet profound geometric relationship will continue to inspire future generations of mathematicians, engineers, and designers.
Latest Posts
Latest Posts
-
Is 2 A Factor Of 73
Apr 09, 2025
-
Which Gas Is The Most Abundant In The Atmosphere
Apr 09, 2025
-
What Is The Lcm Of 18 And 16
Apr 09, 2025
-
Is 97 A Prime Or Composite Number
Apr 09, 2025
-
How Many Feet Is 31 Inches
Apr 09, 2025
Related Post
Thank you for visiting our website which covers about Equilateral Triangle Inscribed In A Circle . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.