Does A Hexagon Have Rotational Symmetry
Juapaving
Apr 04, 2025 · 5 min read
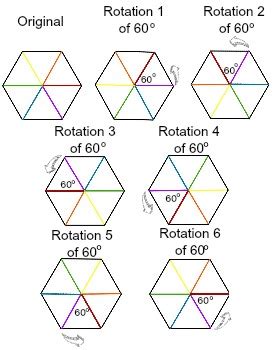
Table of Contents
Does a Hexagon Have Rotational Symmetry? A Deep Dive into Geometric Transformations
Rotational symmetry, a captivating concept in geometry, describes the ability of a shape to be rotated around a central point and still appear identical to its original form. This article delves into the fascinating world of rotational symmetry, focusing specifically on hexagons. We'll explore the definition of rotational symmetry, how to identify it, and definitively answer the question: Does a hexagon have rotational symmetry? Furthermore, we will explore different types of hexagons and their symmetry properties, providing a comprehensive understanding of this geometric concept.
Understanding Rotational Symmetry
Before we delve into the specifics of hexagons, let's establish a clear understanding of rotational symmetry. A shape possesses rotational symmetry if it can be rotated by a certain angle (less than 360 degrees) about a central point, and still look exactly the same as it did before the rotation. This central point is called the center of rotation. The angle of rotation is crucial; it represents the smallest angle by which the shape can be rotated to achieve self-congruence. The number of times the shape maps onto itself during a full 360-degree rotation is called the order of rotational symmetry.
For example, a square has rotational symmetry of order 4. It can be rotated by 90, 180, and 270 degrees and still look identical. A circle, on the other hand, possesses infinite rotational symmetry, as it looks the same after any rotation around its center.
Identifying Rotational Symmetry
Identifying rotational symmetry involves a systematic approach:
- Locate the center of rotation: This is usually the geometric center of the shape, but it's crucial to verify this.
- Determine the angles of rotation: Experiment with rotating the shape by different angles (starting with smaller angles like 30, 45, 60, 90, etc.) Observe whether the rotated shape aligns perfectly with the original.
- Count the number of times the shape maps onto itself: The number of distinct angles that result in self-congruence is the order of rotational symmetry.
Regular Hexagons and Rotational Symmetry
A regular hexagon is a six-sided polygon with all sides equal in length and all interior angles equal (120 degrees). Let's analyze its rotational symmetry:
- Center of Rotation: The center of a regular hexagon is the point equidistant from all its vertices.
- Angles of Rotation: A regular hexagon can be rotated by 60 degrees, 120 degrees, 180 degrees, 240 degrees, and 300 degrees and still appear identical. Each of these rotations maps the hexagon onto itself.
- Order of Rotational Symmetry: Since there are six such rotations (including the 360-degree rotation which is trivial), a regular hexagon has a rotational symmetry of order 6.
Therefore, the answer is a resounding YES. A regular hexagon possesses rotational symmetry.
Irregular Hexagons and Rotational Symmetry
While regular hexagons exhibit a high degree of rotational symmetry, irregular hexagons (those with unequal sides or angles) generally do not possess the same level of symmetry. Some irregular hexagons might have rotational symmetry of order 1 (only a 360-degree rotation leaves it unchanged), while others might have no rotational symmetry at all. The symmetry depends entirely on the specific arrangement of its sides and angles.
For example, consider a hexagon with sides of varying lengths. Unless there's a specific pattern to the unequal lengths and angles that creates rotational symmetry, it will lack rotational symmetry beyond the trivial 360-degree rotation.
Rotational Symmetry vs. Other Types of Symmetry
It's important to differentiate rotational symmetry from other types of symmetry:
- Reflectional Symmetry (Line Symmetry): A shape has reflectional symmetry if it can be folded along a line (called a line of symmetry) to create two identical halves. A regular hexagon has six lines of reflectional symmetry.
- Point Symmetry: A shape has point symmetry if it looks the same when rotated by 180 degrees. This is a special case of rotational symmetry (order 2). A regular hexagon possesses point symmetry.
- Translational Symmetry: This type of symmetry involves repeating a pattern along a line or plane. It is not applicable to isolated hexagons but is relevant when considering tessellations (repeated patterns covering a surface) featuring hexagons.
Hexagons in Nature and Design
The rotational symmetry of hexagons is beautifully illustrated in nature and design:
- Honeycombs: Honeybees construct their honeycombs using hexagonal cells, a testament to nature's efficiency in maximizing space and minimizing material usage. The rotational symmetry of these hexagons contributes to the structural integrity of the honeycomb.
- Snowflakes: While snowflakes are intricate and unique, many exhibit six-fold symmetry, reflecting the underlying hexagonal crystal structure of ice.
- Geometric Patterns: Hexagons are frequently used in artistic designs, architectural structures, and tiling patterns, leveraging their aesthetic appeal and symmetric properties.
Advanced Concepts: Group Theory and Symmetry
The study of symmetry can be deepened through the lens of group theory. Group theory provides a mathematical framework for classifying and analyzing symmetries, including rotational symmetry. The symmetries of a hexagon (including rotations and reflections) form a group called the dihedral group of order 12 (D12). This group captures the complete set of symmetry operations that leave the hexagon unchanged.
Applications of Rotational Symmetry
Understanding rotational symmetry has far-reaching applications beyond purely mathematical contexts:
- Engineering and Design: Symmetrical designs often offer advantages in terms of structural stability, weight distribution, and manufacturing processes.
- Computer Graphics and Animation: Rotational symmetry is crucial for creating efficient and realistic animations and computer-generated images.
- Crystallography: The study of crystal structures relies heavily on understanding symmetry operations, including rotational symmetry.
Conclusion: The Significance of Hexagonal Rotational Symmetry
In conclusion, the question "Does a hexagon have rotational symmetry?" is answered affirmatively, particularly for regular hexagons which exhibit a high order of rotational symmetry (order 6). Understanding rotational symmetry, and the broader concept of symmetry in general, is fundamental to various scientific and artistic fields. The hexagonal structure, with its inherent symmetry, provides efficiency in nature and inspiration in design, demonstrating the profound implications of this geometric concept. From the intricate beauty of snowflakes to the practical applications in engineering and design, the rotational symmetry of hexagons continues to fascinate and inspire. Further exploration into group theory and its application to symmetry opens up even more profound insights into the mathematical elegance and practical utility of this fundamental geometric property.
Latest Posts
Latest Posts
-
Attractions Between Water Molecules Are Called
Apr 11, 2025
-
What Are The Liquids On The Periodic Table
Apr 11, 2025
-
A Solution With A Ph Of 5
Apr 11, 2025
-
How Many Cm Is 30 In
Apr 11, 2025
-
What Is 0 07 As A Fraction
Apr 11, 2025
Related Post
Thank you for visiting our website which covers about Does A Hexagon Have Rotational Symmetry . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.