Does A Cube Have To Have Equal Sides
Juapaving
Apr 07, 2025 · 5 min read
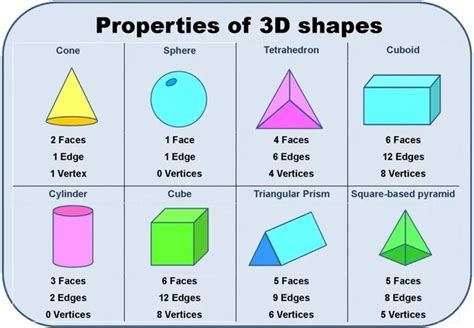
Table of Contents
Does a Cube Have to Have Equal Sides? Exploring the Geometry of Cubes and Cuboids
The simple question, "Does a cube have to have equal sides?" seems straightforward, but it opens a fascinating exploration into the world of geometry, specifically the differences and relationships between cubes and cuboids (also known as rectangular prisms). While the answer is a definitive yes for a cube, understanding why requires a dive into the defining characteristics of these three-dimensional shapes. This article will delve into the geometric properties of cubes and cuboids, clarifying the distinctions and exploring related concepts.
Defining a Cube: The Perfect Polyhedron
A cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. This seemingly simple definition encapsulates several crucial geometric properties:
-
Equal Sides: The most defining characteristic of a cube is that all its sides are equal in length. This is not simply a matter of convention; it's fundamental to its definition. Any deviation from equal side lengths immediately disqualifies the shape from being classified as a cube.
-
Square Faces: Each face of a cube is a perfect square. A square, in turn, is defined as a quadrilateral (four-sided polygon) with all four sides of equal length and four right angles (90-degree angles). Therefore, the equality of sides in a cube extends to the individual sides of each face.
-
Right Angles: The angles formed where the faces of a cube meet are all right angles. This contributes to the overall symmetry and regularity of the cube's structure.
-
Perfect Symmetry: A cube exhibits a high degree of symmetry. It possesses rotational symmetry around various axes, and reflectional symmetry across various planes. This perfect symmetry is a direct consequence of its equal sides and right angles.
Introducing the Cuboid: A Generalization of the Cube
A cuboid, also known as a rectangular prism, is a three-dimensional solid object bounded by six rectangular faces. The key distinction here is that while a cuboid must have rectangular faces, those rectangles do not necessarily have to be squares. This leads to the key differences between cubes and cuboids:
-
Unequal Sides: Unlike a cube, a cuboid can have sides of different lengths. This is the primary defining feature that separates it from a cube. A cuboid can have faces with varying lengths and widths, resulting in a more diverse range of shapes.
-
Rectangular Faces: Each face of a cuboid is a rectangle. Rectangles, unlike squares, have two pairs of equal and parallel sides but the lengths of the sides in each pair can be different.
-
Right Angles: Similar to a cube, all the angles formed where the faces of a cuboid meet are right angles. This maintains a degree of regularity even with the varying side lengths.
-
Less Symmetry: Cuboids generally possess less symmetry than cubes. While they still have some degree of symmetry, it's not as extensive as the perfect symmetry found in a cube. The amount of symmetry will depend on whether certain dimensions are the same. A cuboid with all three dimensions different has less symmetry than a cuboid with only two dimensions the same.
Visualizing the Difference: Cubes vs. Cuboids
Imagine a perfectly stacked box of chocolates. If all the sides of the box are identical squares, you have a cube. However, if the box is longer or wider than it is tall, it's now a cuboid. This simple analogy highlights the core difference: the equality (or lack thereof) of the side lengths.
Many everyday objects can serve as examples of cuboids: brick, a shoebox, a book, and even a room in a house (assuming rectangular walls and a flat ceiling). These objects illustrate the versatility of the cuboid form, which can accommodate various proportions and dimensions. In contrast, finding perfect cubes in nature or everyday life is less common. A perfectly cut diamond may approximate a cube, but true geometrical perfection is rare in the natural world.
Mathematical Implications: Volume and Surface Area
The differences in the shapes of cubes and cuboids also extend to their mathematical properties, particularly in calculating their volume and surface area:
Cube:
-
Volume: The volume of a cube is calculated by cubing the length of one side (side * side * side = side³). Since all sides are equal, this calculation is straightforward.
-
Surface Area: The surface area of a cube is calculated by multiplying the area of one face (side²) by 6 (the number of faces). This is because all six faces are identical squares.
Cuboid:
-
Volume: The volume of a cuboid is calculated by multiplying the length, width, and height (length * width * height). This calculation accommodates the variability of side lengths.
-
Surface Area: The surface area of a cuboid requires summing the areas of all six rectangular faces. Since the faces have different dimensions, the calculation is slightly more complex than for a cube. It generally involves finding the area of each face and adding them together.
Beyond the Basics: Higher Dimensions and Applications
The concept of cubes and cuboids extends beyond basic three-dimensional geometry. In higher-dimensional mathematics, analogous shapes exist (hypercubes, for instance). These concepts find applications in various fields, including:
-
Computer Graphics: Cubes and cuboids are fundamental building blocks in 3D modeling and animation. They serve as primitives for creating more complex shapes and structures.
-
Physics and Engineering: These shapes are frequently used in physics and engineering calculations, particularly in problems involving volumes, forces, and stresses.
-
Crystallography: Crystal structures often exhibit cubic or cuboidal symmetry, reflecting the underlying atomic arrangements.
-
Game Development: Cubes and cuboids are commonly employed in game development for world-building and level design.
Conclusion: The Cube’s Defining Feature
To reiterate the central point: a cube must have equal sides. This fundamental property distinguishes it from the more general category of cuboids, which allows for varying side lengths. While both shapes share some common geometric features like right angles and rectangular faces (in the case of the cube, the faces are square which is a specific case of a rectangle), the equality of sides is the defining characteristic that solidifies a shape’s classification as a cube. Understanding this distinction opens up a deeper appreciation of the richness and complexity of geometric shapes and their applications in various fields. The simplicity of the question belies the depth of geometric concepts it reveals.
Latest Posts
Latest Posts
-
How Many Hours Is 10 Minutes
Apr 08, 2025
-
Why Is It Difficult To Walk On Sand
Apr 08, 2025
-
Demand Pull Vs Cost Push Inflation
Apr 08, 2025
-
Which Two Organisms Are The Most Closely Related
Apr 08, 2025
-
Centre Of Mass Of Equilateral Triangle
Apr 08, 2025
Related Post
Thank you for visiting our website which covers about Does A Cube Have To Have Equal Sides . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.