Derivative Of X 3 X 1
Juapaving
May 13, 2025 · 5 min read
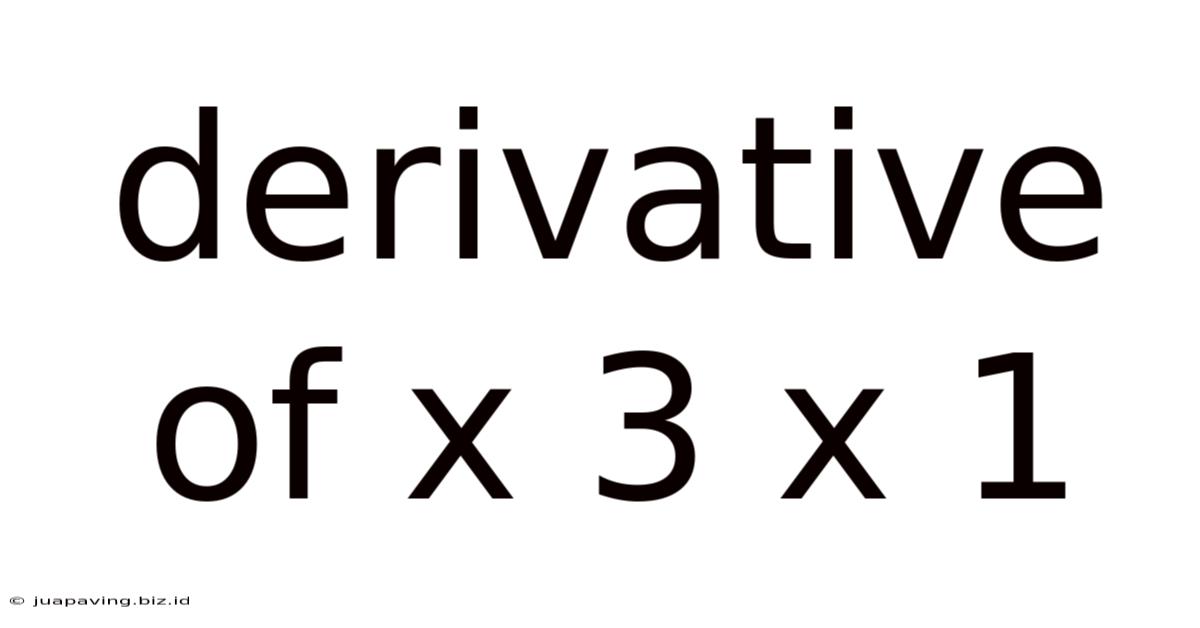
Table of Contents
Delving Deep into the Derivative of x³ - x + 1: A Comprehensive Guide
The derivative of a function is a fundamental concept in calculus, providing insight into the function's instantaneous rate of change. This article will meticulously explore the derivative of the function f(x) = x³ - x + 1, covering its calculation, applications, and interpretations. We'll also delve into the broader context of differentiation and its significance in various fields.
Understanding Derivatives: A Quick Refresher
Before jumping into the specific function, let's solidify our understanding of derivatives. The derivative of a function at a point represents the slope of the tangent line to the function's graph at that point. Geometrically, imagine zooming in infinitely close to a point on a curve; the derivative describes the direction the curve is heading at that precise moment.
Key Concepts:
- Limit: The derivative is defined using the concept of a limit. It represents the value a function approaches as its input approaches a certain value.
- Instantaneous Rate of Change: The derivative captures the rate of change at a single instant, unlike the average rate of change over an interval.
- Slope of the Tangent Line: The derivative is numerically equal to the slope of the tangent line to the curve at a given point.
Calculating the Derivative of x³ - x + 1
The function we're analyzing is f(x) = x³ - x + 1. To find its derivative, we'll employ the power rule, a cornerstone of differential calculus. The power rule states that the derivative of xⁿ is nxⁿ⁻¹, where n is a constant.
Let's break down the derivative calculation step-by-step:
-
Derivative of x³: Applying the power rule, the derivative of x³ is 3x³⁻¹ = 3x².
-
Derivative of -x: The derivative of -x (which can be written as -1x¹) is -1x¹⁻¹ = -1.
-
Derivative of 1: The derivative of a constant (in this case, 1) is always 0.
Therefore, combining these results, the derivative of f(x) = x³ - x + 1 is:
f'(x) = 3x² - 1
This simple expression, 3x² - 1, tells us the slope of the tangent line to the curve of f(x) at any given point x.
Applications and Interpretations of the Derivative
The derivative f'(x) = 3x² - 1 has numerous applications across various fields. Let's explore some key interpretations:
1. Finding Critical Points:
Critical points are locations where the derivative is either zero or undefined. These points often correspond to local maxima, minima, or saddle points on the function's graph. To find the critical points of f(x) = x³ - x + 1, we set f'(x) = 0:
3x² - 1 = 0 3x² = 1 x² = 1/3 x = ±√(1/3)
This gives us two critical points: x = √(1/3) and x = -√(1/3). By examining the second derivative, we can determine the nature of these critical points (whether they are maxima or minima).
2. Determining Increasing and Decreasing Intervals:
The derivative's sign indicates whether the function is increasing or decreasing. If f'(x) > 0, the function is increasing; if f'(x) < 0, it's decreasing.
- f'(x) > 0: 3x² - 1 > 0 => x² > 1/3. This inequality holds when x > √(1/3) or x < -√(1/3).
- f'(x) < 0: 3x² - 1 < 0 => x² < 1/3. This inequality holds when -√(1/3) < x < √(1/3).
Therefore, f(x) is increasing for x < -√(1/3) and x > √(1/3), and decreasing for -√(1/3) < x < √(1/3).
3. Finding Tangent Line Equations:
The derivative allows us to find the equation of the tangent line at any point on the curve. The equation of a tangent line is given by:
y - y₁ = m(x - x₁)
Where (x₁, y₁) is a point on the curve and m is the slope (which is given by the derivative at that point).
For example, to find the equation of the tangent line at x = 1:
- f(1) = 1³ - 1 + 1 = 1, so the point is (1, 1).
- f'(1) = 3(1)² - 1 = 2, so the slope is 2.
The equation of the tangent line is:
y - 1 = 2(x - 1) => y = 2x - 1
4. Optimization Problems:
Derivatives are crucial in optimization problems, where we aim to find maximum or minimum values. For example, in engineering or economics, finding the optimal production level or maximizing profit often involves finding the critical points of a relevant function.
5. Rate of Change in Real-World Applications:
The derivative's interpretation as an instantaneous rate of change makes it applicable in various real-world scenarios. Examples include:
- Physics: Calculating velocity (derivative of position) and acceleration (derivative of velocity).
- Economics: Determining marginal cost (derivative of cost function) and marginal revenue (derivative of revenue function).
- Engineering: Analyzing the rate of change of temperature, pressure, or other physical quantities.
Higher-Order Derivatives
We can find higher-order derivatives by repeatedly differentiating the function. The second derivative, f''(x), represents the rate of change of the first derivative, and it provides information about the concavity of the function.
The second derivative of f(x) = x³ - x + 1 is:
f''(x) = d/dx (3x² - 1) = 6x
The second derivative is positive when x > 0 and negative when x < 0. This indicates that the function is concave up for x > 0 and concave down for x < 0.
Conclusion
The derivative of x³ - x + 1, which is 3x² - 1, provides a wealth of information about the original function's behavior. By understanding how to calculate and interpret derivatives, we can analyze a function's critical points, increasing/decreasing intervals, tangent lines, and concavity. This knowledge has broad applications in mathematics, science, engineering, and economics, making the concept of derivatives essential for solving a wide range of problems. This comprehensive exploration should equip you with a strong foundation to tackle more complex derivative problems and appreciate their significance in various fields. Remember, practice is key to mastering the intricacies of calculus, so keep exploring and experimenting with different functions!
Latest Posts
Latest Posts
-
The Number Of Individuals Per Unit Area
May 13, 2025
-
Which Tissue Type Arises From All Three Embryonic Germ Layers
May 13, 2025
-
Which Of The Following Statements About Social Responsibility Is True
May 13, 2025
-
Why Are Coal Petroleum And Natural Gas Called Fossil Fuels
May 13, 2025
-
Does Prokaryotic Cells Have Golgi Apparatus
May 13, 2025
Related Post
Thank you for visiting our website which covers about Derivative Of X 3 X 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.