Define Conditions Under Which Linear Momentum Is Conserved
Juapaving
Apr 04, 2025 · 6 min read
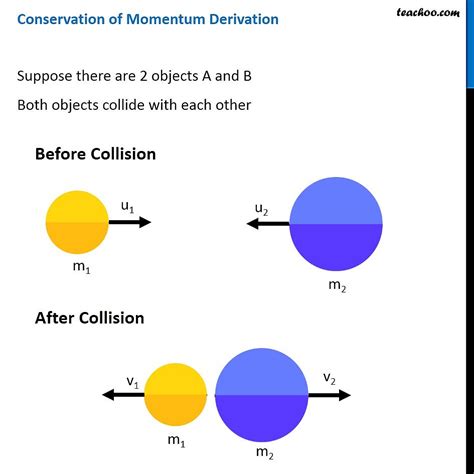
Table of Contents
Defining the Conditions Under Which Linear Momentum is Conserved
Linear momentum, a fundamental concept in physics, describes the quantity of motion an object possesses. Understanding the conditions under which linear momentum is conserved is crucial for analyzing a vast array of physical phenomena, from collisions between billiard balls to the motion of rockets. This article delves deep into the principles governing momentum conservation, exploring its implications and applications.
What is Linear Momentum?
Before exploring the conditions for its conservation, let's define linear momentum. Simply put, linear momentum (p) is the product of an object's mass (m) and its velocity (v):
p = mv
The unit of momentum is typically kilogram-meters per second (kg⋅m/s). It's a vector quantity, meaning it possesses both magnitude and direction. This directionality is vital when analyzing interactions involving multiple objects.
The Law of Conservation of Linear Momentum
The law of conservation of linear momentum states that the total linear momentum of a closed system remains constant if no external forces act on the system. This means that the momentum before an interaction (e.g., a collision) is equal to the momentum after the interaction. Mathematically, this can be represented as:
p<sub>initial</sub> = p<sub>final</sub>
or, more explicitly for a system of multiple particles:
Σp<sub>i,initial</sub> = Σp<sub>i,final</sub>
where Σ represents the sum of the momenta of all particles (i) in the system.
Conditions for Conservation of Linear Momentum: A Detailed Examination
The key condition for the conservation of linear momentum is the absence of external net forces. Let's break down what this entails and explore several related scenarios:
1. Closed System: No External Forces
A closed system is one that doesn't exchange matter or energy with its surroundings. This is the most critical condition. If a net external force acts on the system, it will cause a change in the system's total momentum. This external force could be anything from gravity to friction to applied forces.
Example: Consider two billiard balls colliding on a frictionless table. If we ignore air resistance (a small external force), the system (the two billiard balls) is essentially closed. The total momentum before the collision will equal the total momentum after the collision. However, if the table were not frictionless, friction would act as an external force, altering the momentum.
2. Internal Forces: No Impact on Total Momentum
Internal forces are forces that objects within a system exert on each other. These internal forces, no matter how strong, do not affect the total momentum of the system. This is due to Newton's Third Law of Motion (action-reaction pairs). For every action, there is an equal and opposite reaction. The internal forces cancel each other out when calculating the total momentum of the system.
Example: During the collision of the billiard balls, the force exerted by one ball on the other is an internal force. While this force significantly changes the individual momenta of the balls, the total momentum of the system (both balls) remains unchanged (ignoring external forces).
3. Inelastic vs. Elastic Collisions: Momentum is Always Conserved
Collisions are classified as either elastic or inelastic based on whether kinetic energy is conserved.
-
Elastic collisions: Both momentum and kinetic energy are conserved. Examples include collisions between hard spheres (approximation) or some subatomic particle interactions.
-
Inelastic collisions: Momentum is still conserved, but kinetic energy is not. Some kinetic energy is lost during the collision, often transformed into other forms of energy like heat or sound. A perfectly inelastic collision is one where the objects stick together after the collision.
Example: A car crash is a highly inelastic collision. While the total momentum of the cars before and after the crash is the same (ignoring external forces like friction), a significant amount of kinetic energy is transformed into deformation of the cars, heat, and sound.
4. Explosions: Momentum Remains Conserved
Explosions, seemingly the opposite of collisions, also obey the law of conservation of momentum. The initial momentum of the object before the explosion is zero (if at rest). After the explosion, the fragments will have various velocities and masses, but their vector sum of momenta will still be zero.
Example: A stationary bomb explodes into several fragments. While each fragment has momentum, the vector sum of their momenta will add up to zero, maintaining the initial momentum of the system.
5. Systems with Variable Mass: Rockets
Systems with variable mass, like rockets, present a more complex scenario. However, even here, a modified version of the conservation of momentum law applies. Momentum is not conserved in a simple way because mass is being ejected from the system. The Tsiolkovsky rocket equation accounts for this mass change to calculate the velocity change of the rocket.
Example: A rocket expels propellant downwards. The downwards momentum of the expelled propellant is equal and opposite to the upwards momentum gained by the rocket, resulting in a net change in the rocket's momentum.
6. Relativistic Considerations: Momentum at High Speeds
At speeds approaching the speed of light, Newtonian mechanics break down, and relativistic mechanics must be used. Even in relativity, momentum is conserved, but the definition of momentum is modified:
p = γmv
where γ is the Lorentz factor, given by:
γ = 1 / √(1 - v²/c²)
with c being the speed of light. This relativistic momentum approaches infinity as the velocity approaches the speed of light, preventing objects with mass from ever reaching the speed of light.
Applications of Conservation of Linear Momentum
The conservation of linear momentum has numerous applications across various fields:
-
Collision analysis: Understanding the conditions for momentum conservation allows us to analyze collisions, determining final velocities or impact forces. This is crucial in designing safety systems for vehicles and other impact-prone equipment.
-
Rocket propulsion: The principle of momentum conservation forms the basis of rocket propulsion. By expelling propellant, rockets generate thrust and propel themselves forward.
-
Ballistics: Analyzing projectile trajectories and impacts requires understanding momentum conservation. This is crucial in fields like firearms design, sports analysis (e.g., baseball, golf), and military applications.
-
Nuclear and particle physics: Momentum conservation is a cornerstone of nuclear and particle physics. Analyzing particle interactions requires the application of momentum conservation laws.
-
Fluid mechanics: The conservation of momentum in fluid flow underlies many important phenomena, including the motion of fluids in pipes and the dynamics of airfoils.
Conclusion: A Cornerstone of Physics
The law of conservation of linear momentum is a fundamental principle in physics with far-reaching implications. Understanding the conditions under which it holds true—primarily the absence of external net forces—is essential for accurately analyzing a wide range of physical systems and phenomena. From simple collisions to complex rocket launches, the conservation of momentum provides a powerful tool for understanding and predicting the behavior of physical systems. The nuances of elastic vs. inelastic collisions, variable mass systems, and relativistic considerations further enrich our understanding of this pivotal principle. Mastering the concept of momentum conservation is a key step toward a deeper understanding of the physical world.
Latest Posts
Latest Posts
-
Class 10 History Ch 2 Notes
Apr 05, 2025
-
An Example Of An Oil In Water Emulsion Is
Apr 05, 2025
-
Ficks Law Of Diffusion Transcellular Pathway
Apr 05, 2025
-
What Is The Least Common Multiple Of 12 And 4
Apr 05, 2025
-
How Many Minutes Is 9 Hours
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about Define Conditions Under Which Linear Momentum Is Conserved . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
